题目来源：Leetcode数组中的逆序对

一.题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：
0 <= 数组长度 <= 50000

二.解题思路

2.1.思路确定

在看到题目的第一眼，我首先想到的是暴力法，直接利用一个二层循环，找到每个元素后面比它小的数即构成一个逆序对，但直到我看到限制中数组的长度最大可以到达50000，我立刻放弃了该想法，以我在Leetcode上刷题的经验，肯定会超时的。但我还是”作死”试了一下，果不其然：

像这种类似的题目，算法时间复杂度必定不能超过
$O(n^2)$

O(n2)，于是又一个想法在我脑海中浮现——分治法，这道题的完全符合使用分治法的条件，将数组一分为二，分别在左右两个子数组中寻找逆序对，然后寻找左子数组中的元素和右子数组中的元素构成的逆序对，而且分治法的时间复杂度为
$O(nlogn)$

O(nlogn)完全符合，这样一来算法思路就确定了，下面我将详细介绍如何利用分治法来求解该问题。

2.2.分治法求解过程

分治法求解的套路就不详细说了，无非就是分解，解决，合并，在本题中我直接套用了《算法导论》上归并排序的模板来求解该问题，在这里不得不来安利一波《算法导论》，博主也还在学习，欢迎大家一起来掉头发。

2.2.1.归并排序伪代码

2.2.1.1.主函数

MERGE-SORT(A,p,r) //sort A[p..r] if p < r   q = floor((p + r) / 2) //floor表示向下取整，即取不大于该数的最大整数   MERGE-SORT(A,p,q)   MERGE-SORT(A,q + 1,r)   MERGE(A,p,q,r) 

2.2.1.2.归并函数

MERGE(A,p,q,r) //function：merge A[p..q] and A[q+1,r]  n1 = q - p + 1 //get the length of A[p..q]  n2 = r - q //get the length of A[q+1,r]  创建长度分别为n1 + 1,n2 + 1的数组L,R  L[0..n1 - 1] = A[p..q]#p到q的元素给L  R[0..n2 - 1] = A[q + 1.. r]#q+1到r的元素给R  L[n1] = infinity //infinity意为无穷大  R[n2] = infinity   i = 0  j = 0 for k = p to r   if L[i] <= R[j]    A[k] = L[i]    i = i + 1 else    A[k] = R[j]    j = j + 1 

2.2.2.如何套用归并排序求解

对于两个已经排序的子数组，这里假设为[5,7]，[4,6]，进入归并函数后会在两个子数组后加上一个无穷大(Inifity)，这样左右子数组中的元素就都能弹出来：

由于，左右子数组都是有序的，当左子数组当前元素小于右子数组当前元素时，将做左子数组当前元素取出，这时我们已经可以找出左子数组当前元素构成的逆序对了，即用右子数组当前索引 – 右子数数字起始索引。为啥这样就可以了呢？理由很简单，归并过程中会不断取出左右子数组中较小的元素，而现在取的左子数组元素肯定比之前取出的右子数组元素要大。

示例求解过程

Step0：起始状态

Step1：取出右子数组中的元素4放入结果数组

Step2：取出左子数组中的元素5放入结果数组，此时逆序对增加1(右子数组当前元素索引 – 右子数组起始索引 = 1)

Step3：取出右子数的元素6放于结果数组

Ste4：取出左子数组的元素7放在结果数组，逆序对增加2（有子数组当前索引 – 右子数组起始索引 = 2），此时原数组中的元素都遍历完了，本次寻找结束。

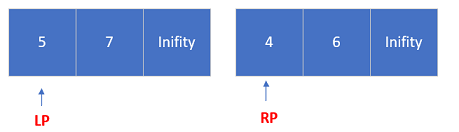
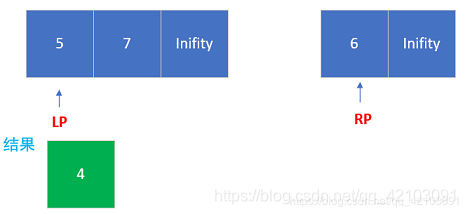
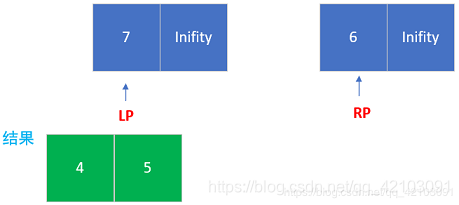
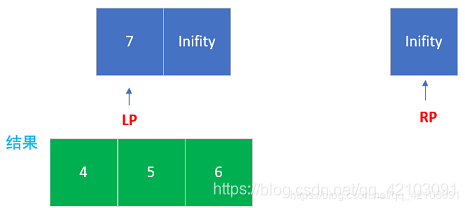
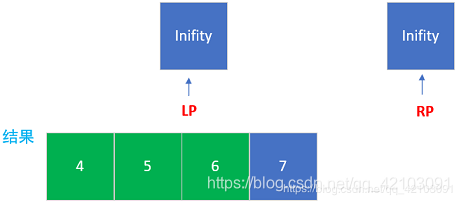
三.代码示例

class Solution: def reversePairs(self, nums: List[int]) -> int: if nums == []:#输入为空 return 0         self.count = 0         self.divide(nums,0,len(nums) - 1) return self.count      def merge(self,nums,start,mid,end): #使用10000000000000000000000代表无穷大         L = nums[start:mid+1] + [10000000000000000000000]         R = nums[mid+1:end+1] + [10000000000000000000000]         i = j = 0         pos = start         for k in range(start,end+1): if L[i] <= R[j]:                 nums[pos] = L[i]                 self.count += j                 i += 1 else:                 nums[pos] = R[j]                 j += 1             pos += 1 def divide(self,nums,left,right): if left == right: return else:             mid = (left + right) // 2             self.divide(nums,left,mid)             self.divide(nums,mid + 1,right)             self.merge(nums,left,mid,right) 

要是觉得不错的话点个赞吧，码文不易，请多支持博主！！！