运筹学整数规划matlab程序Ginger的博客-

Gomory函数

function [X,Z,AAA,BBB] = Gomory(A,B,C,D) % 割平面法的实现 % X: 目标函数的最优解 % Z: 目标函数的极小值 % AAA:满足整数条件的最终表中的系数矩阵 % BBB:满足整数条件的最终表中的常数列向量 % A: 约束函数的系数矩阵，输入前需保证每个约束条件均为＜或≤号 % B: 约束函数的常数列向量，可以有负值 % C: 目标函数的系数向量 % D:求max为1，min为0 if D==0     C=-C; end [c,d]=size(A); BIndex=d+1:1:d+c;%给原始的问题添加c个松弛变量，并用BIndex来记录基向量的下标 for i=1:c     for j=d+1:d+c         if i==j-d             A(i,j)=1;         else             A(i,j)=0;  %更新系数矩阵A         end     end end for i=d+1:1:d+c     C(1,i)=0;   %更新价值系数C end [X,Z,AA,BB,BIndex] = DCXF(A,B,C,BIndex); flag_xunhuan=1;%用作循环开始的条件 while flag_xunhuan     [a,b]=size(X);     flag_zhengshu=1;%是否满足整数条件的标志     for i=1:a         if abs(round(X(i))-X(i))>=1e-3             flag_zhengshu=0;%若不满足整数条件，flag_zhengshu跳变为0；若满足整数条件，flag_zhengshu保持为1             break         end     end     if flag_zhengshu==1         disp('已找到整数最优解：')         flag_xunhuan=0;%改变flag_xunhuan，不再进行循环         if D==0             Z=-Z;         end         AAA=AA;         BBB=BB;     else                %若解不为整数，寻找割平面。          [m,n]=size(AA);          max_chazhi=0;          for i=1:m %循环遍历b矩阵，找出和整数相差最大的那个数和它所在的位置              if BB(i)-floor(BB(i))>max_chazhi                  max_chazhi=BB(i)-floor(BB(i));                  max_chazhi_weizhi=i;              end          end          AA=cat(1,AA,zeros(1,n));%以下操作是对矩阵进行扩展，AA矩阵末尾增加一行一列，BB矩阵末尾增加一行          AA=cat(2,AA,zeros(m+1,1));          AA(m+1,n+1)=1;          BB=cat(1,BB,zeros(1,1));           C=cat(2,C,zeros(1,1));          BIndex=cat(2,BIndex,zeros(1,1));          for i=1:n  %以下操作是增加新的约束条件（即寻找的割平面）              AA(m+1,i)=-(AA(max_chazhi_weizhi,i)-floor(AA(max_chazhi_weizhi,i)));          end          BB(m+1,1)=-(BB(max_chazhi_weizhi)-floor(BB(max_chazhi_weizhi)));          BIndex(m+1)=n+1;          [X,Z,AA,BB,BIndex] = DCXF(AA,BB,C,BIndex);%对增加约束条件后的问题用单纯形法求最优解     end end end 

Gomory中调用了DCXF函数

function [X,Z,AA,BB,BIndex] = DCXF(A,B,C,BIndex) % 单纯形法的实现(包括对偶单纯形法)，需自行添加好松弛变量 % X: 目标函数的最优解 % Z: 目标函数的极小值 % AA:最终表中的系数矩阵 % BB:最终表中的常数列向量 % A: 约束函数的系数矩阵 % B: 约束函数的常数列向量 % C: 目标函数的系数向量 % BIndex: 记录基变量的下标 flag=1; Z=0; [m,n]=size(A); if m>n     disp('系数矩阵不符合要求,无法进行计算。')     X=zeros(1,n);     return  end     while flag         Cb = C(BIndex);             % 基矩阵对应的目标值b         Zj = (Cb)*A;         Sigmaj =C-Zj;                   %判别数σ         X=zeros(n,1);         if max(Sigmaj)<=0           %若满足最优性             if min(B)>=0            %若满足可行性                 for i=1:m                     X(BIndex(i))=B(i);                 end                 for i=1:n                     Z=Z+(C(i)*X(i));                 end                 AA=A;                 BB=B;                 flag = 0;   %同时满足最优性与可行性的情况下才会进行到这一步，使得flag=0，不再进行下次循环。             else          %若已满足最优性，但不满足可行性，使用对偶单纯形法                 [~,h1]=min(B);%获得换出基变量的位置                 for i=1:n                     if A(h1,i)<0                         P(i)=Sigmaj(i)/A(h1,i);                     else                         P(i)=inf;                     end                 end                 [~,h2]=min(P);%确定换入变量的位置                 BIndex(h1)=h2;%新的基变量                 E=[B,A];           %B,A合成一个新的矩阵                 E(h1,:)=E(h1,:)/A(h1,h2);%将E中h1行，除以主元素（即A中h1行，h2列的那个数）；                 for i=1:m                   %更新E                     if(i==h1)                         continue                     end                     E(i,:)=E(i,:)-A(i,h2)*E(h1,:);%将E进行初等行变换                 end                 B=E(1:m,1); %将E拆开为新的A和B                 A=E(1:m,2:n+1);             end %至此，有关可行性的判别与修正算法已结束             else                    %若不满足最优性，继续进行迭代                  [~, k1] = max(Sigmaj); %获得换入基变量的位置                  for i=1:m                      if A(i,k1)>0                         Q(i)=B(i)/A(i,k1);                      else                          Q(i)=inf;%                      end                     end                  [~, k2]=min(Q);    %获得换出基变量的位置                  BIndex(k2)=k1;     %新的基变量                  E=[B,A];           %B,A合成一个新的矩阵                  E(k2,:)=E(k2,:)/A(k2,k1); %将E中k2行，除以主元素（即A中k2行，k1列的那个数）；                  for i=1:m                   %更新E                      if(i==k2)                          continue;                      end                      E(i,:)= E(i,:)-A(i,k1)*E(k2,:);%将E进行初等行变换                  end                  B=E(1:m,1); %将E拆开为新的A和B                  A=E(1:m,2:n+1);         end %至此，有关最优性的判别与修正算法已结束     end end 

举个例子

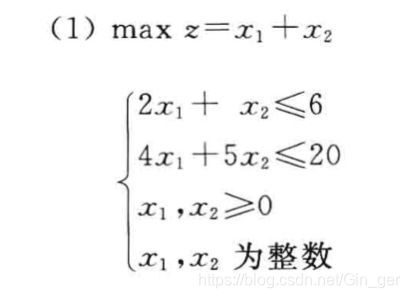
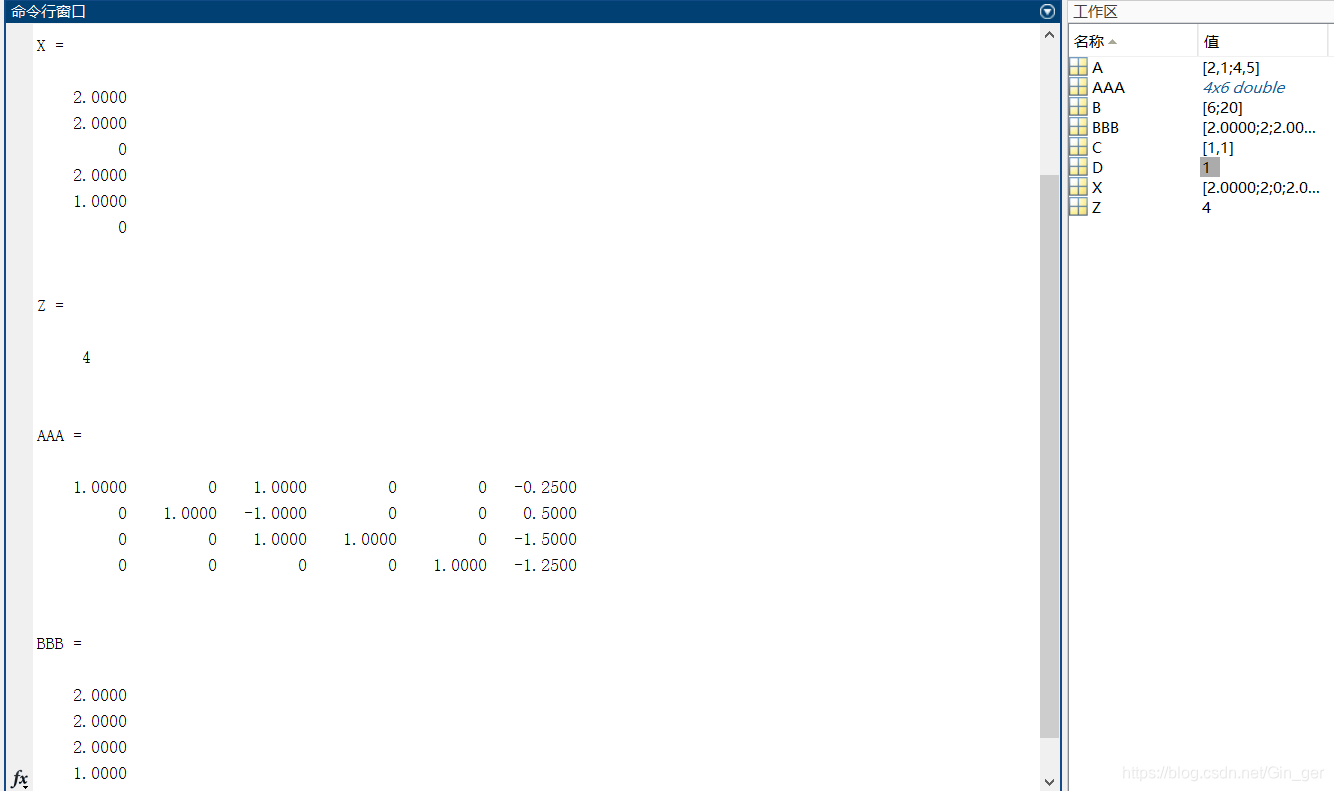
matlab命令窗口参数输入，执行函数，得到最优解