图

图的基本介绍

为什么要有图

• 前面我们学了线性表和树，线性表局限于一个直接前驱和一个直接后继的关系，树也只能有一个直接前驱也就是父节点。
• 当我们需要表示多对多的关系时， 这里我们就用到了图。

图的举例说明

• 图是一种数据结构，其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。 结点也可以称为顶点。如图：
  

图的常用概念

图的表示方式

图的表示方式有两种：二维数组表示（邻接矩阵）；链表表示（邻接表）。

邻接矩阵

• 邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是的row和col表示的是1…n个点。
  

邻接表

• 邻接矩阵需要为每个顶点都分配n个边的空间，其实有很多边都是不存在，会造成空间的一定损失。
• 邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成。
  
• 说明：

* 标号为0的结点的相关联的结点为 1 2 3 4 * 标号为1的结点的相关联结点为0 4 * 标号为2的结点相关联的结点为 0 4 5 

快速入门案例

需求

• 代码实现如下图结构：
  
• 思路分析：存储顶点用String，使用 ArrayList (2) 保存矩阵 int[][] matrix

代码实现

public class GraphDemo { static class Graph { /**          * 存储顶点的集合          */ private List<String> vertices; /**          * 存储边          */ private int[][] matrix; /**          * 边的个数          */ private int edgeCount; Graph(int n) { // 初始化             matrix = new int[n][n];             vertices = new ArrayList<>(n);             edgeCount = 0; } /**          * 添加顶点          */ void addVertex(String vertex) {             vertices.add(vertex); } /**          * 添加边          */ void addEdge(int v1, int v2, int weight) {             matrix[v1][v2] = weight;             matrix[v2][v1] = weight;             edgeCount++; } /**          * 返回结点的个数          */ int getVertexCount() { return vertices.size(); } /**          * 返回边的个数          */ int getEdgeCount() { return edgeCount; } /**          * 返回结点i(下标)对应的数据          */         String getValueByIndex(int i) { return vertices.get(i); } /**          * 返回v1和v2的权值          */ int getWeight(int v1, int v2) { return matrix[v1][v2]; } /**          * 显示图对应的邻接矩阵          */ void show() { for (int[] arr : matrix) {                 System.out.println(Arrays.toString(arr)); } } } public static void main(String[] args) { // 结点的个数 int n = 5; // 结点         String[] vs = {"A", "B", "C", "D", "E"}; // 创建图         Graph graph = new Graph(n); // 循环添加顶点 for (String v : vs) {             graph.addVertex(v); } // 添加边 // A-B A-C B-C B-D B-E         graph.addEdge(0, 1, 1);         graph.addEdge(0, 2, 1);         graph.addEdge(1, 2, 1);         graph.addEdge(1, 3, 1);         graph.addEdge(1, 4, 1); // 显示         graph.show(); } } 

• 测试输出：

[0, 1, 1, 0, 0] [1, 0, 1, 1, 1] [1, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] 

图的遍历

所谓图的遍历，即是对结点的访问。一个图有那么多个结点，如何遍历这些结点，需要特定策略，一般有两种访问策略：深度优先遍历、广度优先遍历。

深度优先遍历

基本介绍

图的深度优先搜索**(Depth First Search，简称 DFS)**

• 深度优先遍历，从初始访问结点出发，初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点， 可以这样理解：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
• 我们可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。
• 显然，深度优先搜索是一个递归的过程。

代码实现

• 算法步骤：

* 访问初始结点v，并标记结点v为已访问 * 查找结点v的第一个邻接结点w * 若w存在，则继续执行4，如果w不存在，则回到第1步，将从v的下一个结点继续 * 若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123） * 查找结点v的w邻接结点的下一个邻接结点，转到步骤3 

• 具体案例：要求对下图进行深度优先搜索，从A开始遍历
  
• 具体实现：

public class GraphDemo { static class Graph { /**          * 存储顶点的集合          */ private List<String> vertices; /**          * 存储边          */ private int[][] matrix; /**          * 边的个数          */ private int edgeCount; /**          * 定义一个数组boolen[]，记录某个结点是否被访问          */ private boolean[] isVisited; Graph(int n) { // 初始化             matrix = new int[n][n];             vertices = new ArrayList<>(n);             edgeCount = 0;             isVisited = new boolean[n]; } /**          * 添加顶点          */ void addVertex(String vertex) {             vertices.add(vertex); } /**          * 添加边          */ void addEdge(int v1, int v2, int weight) {             matrix[v1][v2] = weight;             matrix[v2][v1] = weight;             edgeCount++; } /**          * 返回结点的个数          */ int getVertexCount() { return vertices.size(); } /**          * 返回边的个数          */ int getEdgeCount() { return edgeCount; } /**          * 返回结点i(下标)对应的数据          */         String getValueByIndex(int i) { return vertices.get(i); } /**          * 返回v1和v2的权值          */ int getWeight(int v1, int v2) { return matrix[v1][v2]; } /**          * 显示图对应的邻接矩阵          */ void show() { for (int[] arr : matrix) {                 System.out.println(Arrays.toString(arr)); } } /**          * 得到第一个邻接结点的下标 w          */ int getFirstNeighbor(int index) { for (int j = 0; j < vertices.size(); j++) { if (matrix[index][j] > 0) { return j; } } return -1; } /**          * 根据前一个邻接结点的下标来获取下一个邻接结点          */ int getNextNeighbor(int v1, int v2) { for (int j = v2 + 1; j < vertices.size(); j++) { if (matrix[v1][j] > 0) { return j; } } return -1; } /**          * 清空访问记录          */ void clearVisited() { for (int i = 0; i < isVisited.length; i++) {                 isVisited[i] = false; } } /**          * 对dfs进行一个重载，遍历我们所有的结点，并进行dfs          */ void dfs() { // 遍历所有的结点，进行dfs【回溯】 for (int i = 0; i < getVertexCount(); i++) { if (!isVisited[i]) { dfs(isVisited, i); } } // 遍历结束后把isVisited中的记录清空、便于第二次遍历 clearVisited();             System.out.println(); } /**          * 对一个结点进行深度优先遍历          * @param i 第一次就是0          */ private void dfs(boolean[] isVisited, int i) { // 首先访问该结点，并输出             System.out.print(getValueByIndex(i) + " -> "); // 将该结点设置为已访问             isVisited[i] = true; // 查找结点i的第一个邻接结点w int w = getFirstNeighbor(i); while (w != -1) { if (!isVisited[w]) { dfs(isVisited, w); } // 如果w已经被访问                 w = getNextNeighbor(i, w); } } } public static void main(String[] args) { // 结点的个数 int n = 5; // 结点         String[] vs = {"A", "B", "C", "D", "E"}; // 创建图         Graph graph = new Graph(n); // 循环添加顶点 for (String v : vs) {             graph.addVertex(v); } // 添加边 // A-B A-C B-C B-D B-E         graph.addEdge(0, 1, 1);         graph.addEdge(0, 2, 1);         graph.addEdge(1, 2, 1);         graph.addEdge(1, 3, 1);         graph.addEdge(1, 4, 1); // 显示         graph.show(); // 测试一下DFS         System.out.println("深度优先遍历：");         graph.dfs(); } } 

• 结果输出：

[0, 1, 1, 0, 0] [1, 0, 1, 1, 1] [1, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] 深度遍历： A -> B -> C -> D -> E ->  

广度优先遍历

基本介绍

图的广度优先搜索(Broad First Search)，类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点。

代码实现

• 算法步骤：

* 访问初始结点v并标记结点v为已访问 * 结点v入队列 * 当队列非空时，继续执行，否则算法结束 * 出队列，取得队头结点u * 查找结点u的第一个邻接结点w * 若结点u的邻接结点w不存在，则转到步骤3；否则循环执行以下三个步骤： * ① 若结点w尚未被访问，则访问结点w并标记为已访问 * ② 结点w入队列  * ③ 查找结点u的继w邻接结点后的下一个邻接结点w，转到步骤6 

• 具体实现：

/**  * 广度优先遍历  */ public void bfs() { // 遍历所有的结点，进行bfs【回溯】 for (int i = 0; i < getVertexCount(); i++) { if (!isVisited[i]) { bfs(isVisited, i); } } // 遍历结束后把isVisited中的记录清空、便于第二次遍历 clearVisited();     System.out.println(); } /**  * 对一个结点进行广度优先遍历  */ private void bfs(boolean[] isVisited, int i) { // u:队列的头结点对应的下标,w:邻接结点 int u, w; // 队列：记录结点访问的顺序     LinkedList<Integer> queue = new LinkedList<>(); // 访问结点     System.out.print(getValueByIndex(i) + " -> ");     isVisited[i] = true; // 将结点加入队列     queue.addLast(i); while (!queue.isEmpty()) { // 取出队列的头结点下标         u = queue.removeFirst(); // 得到第一个邻接结点的下标         w = getFirstNeighbor(u); while (w != -1) { if (!isVisited[w]) {                 System.out.print(getValueByIndex(w) + " -> ");                 isVisited[w] = true; // 入队列                 queue.addLast(w); } // 以u为前驱结点，找w后面的邻接点             w = getNextNeighbor(u, w); // 体现广度优先 } } } public static void main(String[] args) { // 结点的个数 int n = 5; // 结点     String[] vs = {"A", "B", "C", "D", "E"}; // 创建图     Graph graph = new Graph(n); // 循环添加顶点 for (String v : vs) {         graph.addVertex(v); } // 添加边 // A-B A-C B-C B-D B-E     graph.addEdge(0, 1, 1);     graph.addEdge(0, 2, 1);     graph.addEdge(1, 2, 1);     graph.addEdge(1, 3, 1);     graph.addEdge(1, 4, 1); // 显示     graph.show(); // 测试一下DFS     System.out.println("深度优先遍历：");     graph.dfs();     System.out.println("广度优先遍历：");     graph.bfs(); } 

• 结果输出：

[0, 1, 1, 0, 0] [1, 0, 1, 1, 1] [1, 1, 0, 0, 0] [0, 1, 0, 0, 0] [0, 1, 0, 0, 0] 深度优先遍历： A -> B -> C -> D -> E ->  广度优先遍历： A -> B -> C -> D -> E ->  

深度优先 Vs 广度优先

• 应用实例：
  
• 深度优先遍历顺序为：1->2->4->8->5->3->6->7
• 广度优先算法的遍历顺序为：1->2->3->4->5->6->7->8

常用十种算法

非递归二分查找

基本介绍

• 前面我们讲过了二分查找算法，是使用递归的方式，下面我们讲解二分查找算法的非递归方式。
• 二分查找法只适用于从有序的数列中进行查找(比如数字和字母等)，将数列排序后再进行查找。
• 二分查找法的运行时间为对数时间O(㏒₂n) ，即查找到需要的目标位置最多只需要㏒₂n步，假设从[0,99]的队列(100个数，即n=100)中寻到目标数30，则需要查找步数为㏒₂100 , 即最多需要查找7次( 2⁶ < 100 < 2⁷)。

代码实现

public class BinarySearchNoRecur { public static void main(String[] args) { int[] arr = {1, 3, 8, 10, 11, 67, 100}; for (int a : arr) { int index = search(arr, a);             System.out.printf("非递归二分查找 %d, index = %dn", a, index); }         System.out.printf("非递归二分查找 %d, index = %dn", -8, search(arr, -8)); } private static int search(int[] arr, int target) { int left = 0; int right = arr.length - 1; while (left <= right) { int mid = (left + right) / 2; if (arr[mid] == target) { return mid; } else if (arr[mid] > target) {                 right = mid - 1; } else {                 left = mid + 1; } } return -1; } } 

• 结果输出：

非递归二分查找 1, index = 0 非递归二分查找 3, index = 1 非递归二分查找 8, index = 2 非递归二分查找 10, index = 3 非递归二分查找 11, index = 4 非递归二分查找 67, index = 5 非递归二分查找 100, index = 6 非递归二分查找 -8, index = -1 

分治算法

基本介绍

• 分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……
• 分治算法可以求解的一些经典问题：二分搜索、大整数乘法、棋盘覆盖、合并排序、快速排序、线性时间选择、最接近点对问题、循环赛日程表、汉诺塔

基本步骤

• 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。
• 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
• 合并：将各个子问题的解合并为原问题的解。

算法的设计模式

• 其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。ADHOC§是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC§求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法，用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。

最佳实践-汉诺塔

基本介绍

• 汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
• 假如每秒钟一次，共需多长时间呢？移完这些金片需要5845.54亿年以上，太阳系的预期寿命据说也就是数百亿年。真的过了5845.54亿年，地球上的一切生命，连同梵塔、庙宇等，都早已经灰飞烟灭。
  

思路分析

• 如果只有一个盘， A->C；
• 如果我们有 n >= 2 情况，我们总是可以看做是两个盘：一个是最下边的盘，一个是上面所有的盘【整体思想】；
• ① 先把最上面的盘 A->B
• ② 把最下边的盘 A->C
• ③ 把B塔的所有盘 从 B->C

代码实现

public class Hanoitower { public static void main(String[] args) { hanoiTower(5, 'A', 'B', 'C'); } private static void hanoiTower(int num, char a, char b, char c) { if (num == 1) { // 1、如果只有一个盘， A->C             System.out.printf("第 %d 个盘从 %s -> %sn", num, a, c); } else { // 2、如果我们有 n >= 2 情况，我们总是可以看做是两个盘：一个是最下边的盘，一个是上面所有的盘 // 先把最上面的盘 A->B hanoiTower(num - 1, a, c, b); // 把最下边的盘 A->C             System.out.printf("第 %d 个盘从 %s -> %sn", num, a, c); // 把B塔的所有盘 从 B->C hanoiTower(num - 1, b, a, c); } } } 

• 测试输出：

第 1 个盘从 A -> C 第 2 个盘从 A -> B 第 1 个盘从 C -> B 第 3 个盘从 A -> C 第 1 个盘从 B -> A 第 2 个盘从 B -> C 第 1 个盘从 A -> C 第 4 个盘从 A -> B 第 1 个盘从 C -> B 第 2 个盘从 C -> A 第 1 个盘从 B -> A 第 3 个盘从 C -> B 第 1 个盘从 A -> C 第 2 个盘从 A -> B 第 1 个盘从 C -> B 第 5 个盘从 A -> C 第 1 个盘从 B -> A 第 2 个盘从 B -> C 第 1 个盘从 A -> C 第 3 个盘从 B -> A 第 1 个盘从 C -> B 第 2 个盘从 C -> A 第 1 个盘从 B -> A 第 4 个盘从 B -> C 第 1 个盘从 A -> C 第 2 个盘从 A -> B 第 1 个盘从 C -> B 第 3 个盘从 A -> C 第 1 个盘从 B -> A 第 2 个盘从 B -> C 第 1 个盘从 A -> C 

动态规划算法

动态规划算法介绍

• 动态规划(Dynamic Programming)算法的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法。
• 动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
• 与分治法不同的是：适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )。
• 动态规划可以通过填表的方式来逐步推进，得到最优解。

应用场景-背包问题

• 有一个背包，容量为4磅 ， 现有如下物品：
  
• 要求达到的目标为装入的背包的总价值最大，并且重量不超出。
• 要求装入的物品不能重复。

思路分析和图解

• 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分01背包和完全背包(完全背包指的是：每种物品都有无限件可用)。
• 这里的问题属于01背包，即每个物品最多放一个。而无限背包可以转化为01背包。
• 算法的主要思想：利用动态规划来解决。每次遍历到的第i个物品，根据 w[i] 和 v[i] 来确定是否需要将该物品放入背包中。即对于给定的n个物品，设v[i]、w[i]分别为第i个物品的价值和重量，C为背包的容量。再令v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果：
• ① v[i][0]=v[0][j]=0：表示填入表 第一行和第一列是0
• ② 当 w[i]>j 时，v[i][j]=v[i-1][j]：当准备加入新增的商品的容量大于当前背包的容量时，就直接使用上一个单元格的装入策略
• ③ 当 j>=w[i] 时，v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} ：当准备加入的新增的商品的容量小于等于当前背包的容量，则装入的方式为：

* v[i-1][j]：就是上一个单元格的装入的最大值 * v[i]：表示当前商品的价值 * v[i-1][j-w[i]]：装入i-1商品，到剩余空间j-w[i]的最大值 * 当 j>=w[i] 时：v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} 

代码实现

public class KnapsackProblem { public static void main(String[] args) { // 物品重量 int[] w = {1, 4, 3}; // 物品的价值 int[] val = {1500, 3000, 2000}; // 背包的容量 int m = 4; // 物品的个数 int n = val.length; // 为了记录存放商品的情况， int[][] path = new int[n + 1][m + 1]; // 创建二维数组 // v[i][j]: 表示在前i个物品中，能够转入容量为j的背包中的最大价值 int[][] v = new int[n + 1][m + 1]; // 1、初始化第一行、第一列，在本程序中可以不处理，因为默认就是0 for (int i = 0; i < v.length; i++) {             v[i][0] = 0; } for (int i = 0; i < v[0].length; i++) {             v[0][i] = 0; } // 2、根据前面得到的公式来动态规划处理 for (int i = 1; i < v.length; i++) { for (int j = 1; j < v[0].length; j++) { // 公式 if (w[i - 1] > j) {                     v[i][j] = v[i - 1][j]; } else { // 说明：因为i是从1开始的，因此公式需要调整成如下 //                    v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]); // 为了记录商品存放到背包的情况，不能直接用上面的公式 if (v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {                         v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];                         path[i][j] = 1; } else {                         v[i][j] = v[i - 1][j]; } } } } for (int i = 0; i < v.length; i++) { for (int j = 0; j < v[i].length; j++) {                 System.out.print(v[i][j] + " "); }             System.out.println(); } // 输出最后我们是放入了哪些商品 // 下面这样遍历，会输出所有放入背包的情况，但其实我们只需要最后放入的 //        for (int i = 0; i < path.length; i++) { //            for (int j = 0; j < path[i].length; j++) { //                if (path[i][j] == 1) { //                    System.out.printf("第%d个商品放入背包n", i); //                } //            } //        } int i = path.length - 1; int j = path[0].length - 1; while (i > 0 && j > 0) { if (path[i][j] == 1) {                 System.out.printf("第%d个商品放入背包n", i);                 j -= w[i - 1]; }             i--; } } } 

• 测试输出：

0 0 0 0 0  0 1500 1500 1500 1500  0 1500 1500 1500 3000  0 1500 1500 2000 3500  第3个商品放入背包 第1个商品放入背包 

KMP算法

应用场景

• 有一个字符串 str1= ““硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好””，和一个子串 str2=“尚硅谷你尚硅你”；
• 现在要判断 str1 是否含有 str2, 如果存在，就返回第一次出现的位置, 如果没有，则返回-1。

暴力匹配算法

如果用暴力匹配的思路，并假设现在str1匹配到 i 位置，子串str2匹配到 j 位置，则有：

• 如果当前字符匹配成功（即str1[i] == str2[j]），则i++，j++，继续匹配下一个字符；
• 如果失配（即str1[i]! = str2[j]），令i = i – (j – 1)，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。
• 用暴力方法解决的话就会有大量的回溯，每次只移动一位，若是不匹配，移动到下一位接着判断，浪费了大量的时间。(不可行!)；
• 代码实现：

public class ViolenceMatch { public static void main(String[] args) {         System.out.println(match("硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好", "尚硅谷你尚硅你")); } private static int match(String src, String target) { int i = 0, j = 0; while (i < src.length() && j < target.length()) { if (src.charAt(i) == target.charAt(j)) {                 i++;                 j++; } else {                 i = i - (j - 1);                 j = 0; } if (j == target.length()) { return i - j; } } return -1; } } // 结果：15 

基本介绍

• KMP是一个解决模式串在文本串是否出现过，如果出现过，最早出现的位置的经典算法。
• Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串P 的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法。
• KMP方法算法就利用之前判断过信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过next数组找到，前面匹配过的位置，省去了大量的计算时间。
• 参考资料：添加链接描述

最佳实践-字符串匹配问题

需求

• 有一个字符串 str1= “BBC ABCDAB ABCDABCDABDE”，和一个子串 str2=“ABCDABD”。
• 现在要判断 str1 是否含有 str2, 如果存在，就返回第一次出现的位置, 如果没有，则返回-1。
• 要求：使用KMP算法完成判断，不能使用简单的暴力匹配算法。

思路分析

• ① 首先，用Str1的第一个字符和Str2的第一个字符去比较，不符合则关键词向后移动一位。
  
• ② 重复第一步，还是不符合，再后移。
  
• ③ 一直重复，直到Str1有一个字符与Str2的第一个字符符合为止。
  
• ④ 接着比较字符串和搜索词的下一个字符，还是符合。
  
• ⑤ 遇到Str1有一个字符与Str2对应的字符不符合。
  
• ⑥ 这时候，想到的是继续遍历Str1的下一个字符，重复第1步。其实是很不明智的，因为此时BCD已经比较过了，没有必要再做重复的工作，一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是”ABCDAB”。KMP 算法的想法是，设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，继续把它向后移，这样就提高了效率。
  
• ⑦ 怎么做到把刚刚重复的步骤省略掉？可以对Str2计算出一张《部分匹配表》
  
• ⑧ 已知空格与D不匹配时，前面六个字符”ABCDAB”是匹配的。查表可知，最后一个匹配字符B对应的”部分匹配值”为2，因此按照下面的公式算出向后移动的位数：移动位数 = 已匹配的字符数 – 对应的部分匹配值，因为 6 – 2 等于4，所以将搜索词向后移动 4 位。
• ⑨ 因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（“AB”），对应的“部分匹配值”为0。所以，移动位数 = 2 – 0，结果为 2，于是将搜索词向后移 2 位。
  
• ⑩ 因为空格与A不匹配，继续后移一位。
  
• ⑪ 逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 – 2，继续将搜索词向后移动 4 位。
  
• ⑫ 逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 – 0，再将搜索词向后移动 7 位，这里就不再重复了。
  

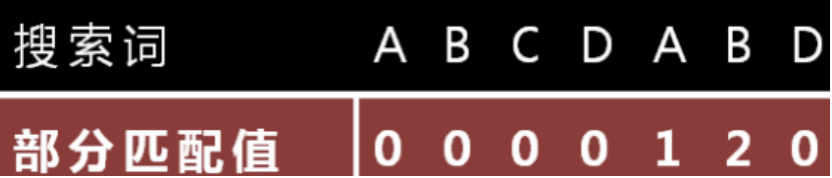
部分匹配表怎么产生？

代码实现

public class KmpMatch { public static void main(String[] args) {         String src = "BBC ABCDAB ABCDABCDABDE";         String target = "ABCDABD"; int[] next = kmpNext(target);         System.out.printf("Next[%s] = %sn", target, Arrays.toString(next)); int index = match(src, target, next);         System.out.println("KMP匹配index = " + index); } /**      * kmp匹配算法      */ private static int match(String src, String target, int[] next) { for (int i = 0, j = 0; i < src.length(); i++) { // kmp 算法的核心 while (j > 0 && src.charAt(i) != target.charAt(j)) {                 j = next[j - 1]; } if (src.charAt(i) == target.charAt(j)) {                 j++; } if (j == target.length()) { // 找到了 return i - j + 1; } } return -1; } /**      * 获取一个字符串(子串)的部分匹配值      */ private static int[] kmpNext(String s) { if (s == null) { return null; } int len = s.length(); // 创建一个数组保存部分匹配值 int[] next = new int[len];         next[0] = 0; for (int i = 1, j = 0; i < len; i++) { // kmp 算法的核心 while (j > 0 && s.charAt(i) != s.charAt(j)) {                 j = next[j - 1]; } if (s.charAt(i) == s.charAt(j)) {                 j++; }             next[i] = j; } return next; } } // 结果输出： // Next[ABCDABD] = [0, 0, 0, 0, 1, 2, 0] // KMP匹配index = 15 

贪心算法

应用场景

• 假设存在下面需要付费的广播台，以及广播台信号可以覆盖的地区。 如何选择最少的广播台，让所有的地区都可以接收到信号。
  

基本介绍

• **贪婪算法(贪心算法)**是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法。
• 贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果。

最佳实践-集合覆盖

思路分析

• 如何找出覆盖所有地区的广播台的集合呢，使用穷举法实现，列出每个可能的广播台的集合，这被称为幂集。假设总的有n个广播台，则广播台的组合总共有2ⁿ -1 个，假设每秒可以计算10个子集， 如图：
  
• 使用贪婪算法，效率高：目前并没有算法可以快速计算得到准备的值， 使用贪婪算法，则可以得到非常接近的解，并且效率高。选择策略上，因为需要覆盖全部地区的最小集合：
• ① 遍历所有的广播电台, 找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区，但没有关系）；
• ② 将这个电台加入到一个集合中(比如ArrayList)，想办法把该电台覆盖的地区在下次比较时去掉；
• ③ 重复第1步直到覆盖了全部的地区。

代码实现

public class GreedyAlgorithm { public static void main(String[] args) { // 创建广播电台，放入Map         Map<String, Set<String>> broadcastMap = new LinkedHashMap<>(8); // 将各个电台放入broadcastMap         broadcastMap.put("K1", newHashSet("北京", "上海", "天津"));         broadcastMap.put("K2", newHashSet("广州", "北京", "深圳"));         broadcastMap.put("K3", newHashSet("成都", "上海", "杭州"));         broadcastMap.put("K4", newHashSet("上海", "天津"));         broadcastMap.put("K5", newHashSet("杭州", "大连")); // 所有地区的集合         Set<String> allAreas = getAllAreas(broadcastMap);         System.out.println("All Areas = " + allAreas); // 创建一个List，存放选择的电台集合         List<String> selects = new ArrayList<>(); // 定义一个临时的集合，在遍历的过程中，存放遍历过程中的电台覆盖的地区和当前还没有覆盖的地区的交集         Set<String> tempSet = new HashSet<>(); // 定义maxKey：保存在一次遍历过程中，能够覆盖最大未覆盖的地区对应的电台的 key // 如果 maxKey 不为 null , 则会加入到 selects         String maxKey; while (allAreas.size() > 0) { // 每进行一次循环，都需要将maxKey置空             maxKey = null; for (String key : broadcastMap.keySet()) {                 tempSet.clear();                 tempSet.addAll(broadcastMap.get(key)); // 求出 tempSet 和 allAreas 集合的交集, 交集会赋给 tempSet                 tempSet.retainAll(allAreas); // 如果当前这个集合包含的未覆盖地区的数量，比 maxKey 指向的集合地区还多，就需要重置 maxKey if (tempSet.size() > 0 && (maxKey == null || tempSet.size() > broadcastMap.get(maxKey).size())) {                     maxKey = key; } } if (maxKey != null) {                 selects.add(maxKey); // 将 maxKey 指向的广播电台覆盖的地区，从 allAreas 去掉                 allAreas.removeAll(broadcastMap.get(maxKey)); } }         System.out.println("得到的结果是:" + selects); } @SafeVarargs private static <E> Set<E> newHashSet(E... elements) { return new HashSet<>(Arrays.asList(elements)); } private static Set<String> getAllAreas(Map<String, Set<String>> broadcastMap) {         Set<String> res = new HashSet<>(); for (Set<String> value : broadcastMap.values()) {             res.addAll(value); } return res; } } // 输出： // All Areas = [成都, 上海, 广州, 天津, 大连, 杭州, 北京, 深圳] // 得到的结果是:[K1, K2, K3, K5] 

注意事项和细节

• 贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但都是相对近似(接近)最优解的结果。
• 比如上题的算法选出的是K1, K2, K3, K5，符合覆盖了全部的地区，但是我们发现 K2, K3,K4,K5 也可以覆盖全部地区，如果K2 的使用成本低于K1，那么我们上题的 K1, K2, K3, K5 虽然是满足条件，但是并不是最优的。

普里姆算法

应用场景

看一个应用场景和问题：

• 胜利乡有7个村庄(A, B, C, D, E, F, G) ，现在需要修路把7个村庄连通。
• 各个村庄的距离用边线表示(权) ，比如 A – B 距离 5公里。
• 问：如何修路保证各个村庄都能连通，并且总的修建公路总里程最短?
• 一种思路是，将10条边，连接即可，但是总的里程数不是最小。正确的思路，就是尽可能的选择少的路线，并且每条路线最小，保证总里程数最少。

最小生成树

修路问题本质就是就是最小生成树问题， 先介绍一下最小生成树(Minimum Cost Spanning Tree)，简称MST。

• 给定一个带权的无向连通图，如何选取一棵生成树，使树上所有边上权的总和为最小，这叫最小生成树。
• N个顶点，一定有N-1条边，包含全部顶点，N-1条边都在图中，如下图：
  
  求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法

基本介绍

• 普利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有(n-1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图。
• 普利姆的算法如下：
• ① 设G=(V,E)是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合。
• ② 若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的visited[u]=1。
• ③ 若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但能构成回路，将顶点vj加入集合U中，将边（ui,vj）加入集合D中，标记visited[vj]=1。
• ④ 重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有n-1条边。

最佳实践-修路问题

思路分析

代码实现

public class PrimCase { /**      * 定义图      */ static class Graph { /**          * 图的顶点数据          */ char[] vertices; /**          * 图的边，采用邻接矩阵          */ int[][] matrix; /**          * 图的顶点数          */ int vertexCount; Graph(int n) {             vertices = new char[n];             matrix = new int[n][n];             vertexCount = n; } } /**      * 定义最小生成树      */ static class MinTreeGraph {         Graph graph; MinTreeGraph(Graph graph) { this.graph = graph; }          MinTreeGraph createGraph(char[] vertices, int[][] matrix) { int vCount = graph.vertexCount; for (int i = 0; i < vCount; i++) {                 graph.vertices[i] = vertices[i];                 System.arraycopy(matrix[i], 0, graph.matrix[i], 0, vCount); } return this; } /**          * 编写普里姆算法，得到最小生成树          *          * @param v 表示从图的第几个顶点开始生成          */ void primTree(int v) { int vCount = graph.vertexCount; // 标记结点是否被访问，1:被访问 int[] visited = new int[vCount];             visited[v] = 1; // 定义v1、v2记录两个顶点的下标 int v1 = -1, v2 = -1; // 定义一个变量，存放最小权值的边 int minW = Integer.MAX_VALUE; for (int k = 1; k < vCount; k++) { // 这个是确定每一次生成的子图，和那个结点的距离最近 for (int i = 0; i < vCount; i++) { // i结点表示被访问过的结点，j结点表示没有访问过的结点 for (int j = 0; j < vCount; j++) { if (visited[i] == 1 && visited[j] == 0 && graph.matrix[i][j] < minW) {                             minW = graph.matrix[i][j];                             v1 = i;                             v2 = j; } } } // for循环结束后，就找到了一条最小的边                 System.out.printf("边 <%s, %s>，权值：%dn", graph.vertices[v1], graph.vertices[v2], minW); // 将当前这个结点标记为已访问                 visited[v2] = 1; // 重置minW                 minW = Integer.MAX_VALUE; } } void show() { for (int[] arr : graph.matrix) {                 System.out.println(Arrays.toString(arr)); } } } public static void main(String[] args) { // 定义图中的顶点和边 char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; int M = Integer.MAX_VALUE; int[][] matrix = new int[][]{ {M, 5, 7, M, M, M, 2}, // A {5, M, M, 9, M, M, 3}, // B {7, M, M, M, 8, M, M}, // C {M, 9, M, M, M, 4, M}, // D {M, M, 8, M, M, 5, 4}, // E {M, M, M, 4, 5, M, 6}, // F {2, 3, M, M, 4, 6, M}, // G };         MinTreeGraph minTreeGraph = new MinTreeGraph(new Graph(vertices.length)) .createGraph(vertices, matrix); //        minTreeGraph.show();          minTreeGraph.primTree(0); } } 

• 结果输出：

边 <A, G>，权值：2 边 <G, B>，权值：3 边 <G, E>，权值：4 边 <E, F>，权值：5 边 <F, D>，权值：4 边 <A, C>，权值：7 

克鲁斯卡尔算法

应用场景

• 公交站问题
  
• 某城市新增7个站点(A, B, C, D, E, F, G) ，现在需要修路把7个站点连通。
• 各个站点的距离用边线表示(权) ，比如 A – B 距离 12公里。
• 问：如何修路保证各个站点都能连通，并且总的修建公路总里程最短?

基本介绍

• 克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。
• **基本思想：**按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。
• **具体做法：**首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

最佳实践-公交站问题

思路分析

• 在含有n个顶点的连通图中选择n-1条边，构成一棵极小连通子图，并使该连通子图中n-1条边上权值之和达到最小，则称其为连通网的最小生成树。
  
• 例如，对于如上图G4所示的连通网可以有多棵权值总和不相同的生成树。
  
• 克鲁斯卡尔算法图解步骤：
  
• 最终最小生成树的边依次是：<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。

克鲁斯卡尔算法分析

根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题：

• 问题一：对图的所有边按照权值大小进行排序。
• 问题二：将边添加到最小生成树中时，怎么样判断是否形成了回路。
• 问题一很好解决，采用排序算法进行排序即可。
• 问题二处理方式是：记录顶点在”最小生成树”中的终点，顶点的终点是”在最小生成树中与它连通的最大顶点”。然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。
• 如何判断是否构成回路-举例说明：
  
• 在将<E,F> <C,D> <D,E>加入到最小生成树R中之后，这几条边的顶点就都有了终点：C的终点是F、D的终点是F、E的终点是F、E的终点是F。【终点：就是将所有顶点按照从小到大的顺序排列好之后；某个顶点的终点就是”与它连通的最大顶点”】
• 因此，接下来，虽然<C,E>是权值最小的边。但是C和E的终点都是F，即它们的终点相同，因此，将<C,E>加入最小生成树的话，会形成回路。这就是判断回路的方式。也就是说，我们加入的边的两个顶点不能都指向同一个终点，否则将构成回路。

代码实现

public class KruskalCase { /**      * 定义图      */ static class Graph { /**          * 图的顶点数据          */ char[] vertices; /**          * 图的边，采用邻接矩阵          */ int[][] matrix; /**          * 图的顶点数          */ int vertexCount; /**          * 图的边数          */ int edgeCount; Graph(int n) {             vertices = new char[n];             matrix = new int[n][n];             vertexCount = n; } } /**      * 定义边      */ static class Edge implements Comparable<Edge> { /**          * 边的起点          */ char fromV; /**          * 边的终点          */ char toV; /**          * 边的权值          */ int weight; Edge(char fromV, char toV, int weight) { this.fromV = fromV; this.toV = toV; this.weight = weight; } @Override public String toString() { return "Edge <" + fromV + "--" + toV + ">=" + weight; } @Override public int compareTo(Edge o) { // 从小到大排序 return this.weight - o.weight; } } /**      * 定义最小生成树      */ static class MinTreeGraph {         Graph graph;         List<Edge> edges = new ArrayList<>(); MinTreeGraph(Graph graph) { this.graph = graph; }          MinTreeGraph createGraph(char[] vertices, int[][] matrix) { int vCount = graph.vertexCount; for (int i = 0; i < vCount; i++) {                 graph.vertices[i] = vertices[i];                 System.arraycopy(matrix[i], 0, graph.matrix[i], 0, vCount); } // 统计边 for (int i = 0; i < vCount; i++) { for (int j = i + 1; j < vCount; j++) { if (matrix[i][j] != MAX) {                         edges.add(new Edge(vertices[i], vertices[j], matrix[i][j])); } } }             graph.edgeCount = edges.size(); return this; }          List<Edge> kruskal() { // 用于保存"已有最小生成树" 中的每个顶点在最小生成树中的终点 int[] ends = new int[graph.edgeCount]; // 创建结果集合, 保存最后的最小生成树             List<Edge> results = new ArrayList<>(); // /遍历 edges 数组，将边添加到最小生成树中时，判断是准备加入的边否形成了回路，如果没有，就加入 rets, 否则不能加入             List<Edge> edges = getSortedEdges(); for (Edge edge : edges) { // 获取边的两个顶点 int formIndex = getPosition(edge.fromV); int toIndex = getPosition(edge.toV); // 分别获取这两个顶点的终点 int fromEnd = getEndIndex(ends, formIndex); int toEnd = getEndIndex(ends, toIndex); // 是否构成回路 if (fromEnd != toEnd) { // 设置fromEnd在"已有最小生成树"中的终点                     ends[fromEnd] = toEnd;                     results.add(edge); } } return results; }          List<Edge> getSortedEdges() {             Collections.sort(edges); return edges; } /**          * 对边进行排序处理          */ void sortEdge() {             Collections.sort(edges); } /**          * 返回顶点的下标          */ int getPosition(char c) { for (int i = 0; i < graph.vertices.length; i++) { if (graph.vertices[i] == c) { return i; } } return -1; } /**          * 获取下标为i的顶点的终点，用于后面判断两个顶点的终点是否相同          *          * @param ends 记录了各个顶点对应的终点是哪个          * @param i    表示传入的顶点对应的下标          */ int getEndIndex(int[] ends, int i) { while (ends[i] != 0) {                 i = ends[i]; } return i; } /**          * 打印边          */ void showEdges() {             System.out.println(edges); } /**          * 打印邻接矩阵          */ void show() {             System.out.println("邻接矩阵："); for (int[] arr : graph.matrix) { for (int a : arr) {                     System.out.printf("%12dt", a); }                 System.out.println(); } } } private static final int MAX = Integer.MAX_VALUE; public static void main(String[] args) { // 定义图中的顶点和边 char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; int[][] matrix = new int[][]{ /*A*//*B*//*C*//*D*//*E*//*F*//*G*/ /*A*/{0, 12, MAX, MAX, MAX, 16, 14}, /*B*/{12, 0, 10, MAX, MAX, 7, MAX}, /*C*/{MAX, 10, 0, 3, 5, 6, MAX}, /*D*/{MAX, MAX, 3, 0, 4, MAX, MAX}, /*E*/{MAX, MAX, 5, 4, 0, 2, 8}, /*F*/{16, 7, 6, MAX, 2, 0, 9}, /*G*/{14, MAX, MAX, MAX, 8, 9, 0}, };         MinTreeGraph minTreeGraph = new MinTreeGraph(new Graph(vertices.length)) .createGraph(vertices, matrix);         minTreeGraph.show(); //        System.out.println(minTreeGraph.graph.edgeCount);         System.out.println("排序前：");         minTreeGraph.showEdges();         minTreeGraph.sortEdge();         System.out.println("排序后：");         minTreeGraph.showEdges();          List<Edge> edges = minTreeGraph.kruskal();         System.out.println("克鲁斯卡尔最小生成树结果:" + edges); } } 

• 结果输出：

邻接矩阵：            0           12   2147483647   2147483647   2147483647           16           14            12            0           10   2147483647   2147483647            7   2147483647    2147483647           10            0            3            5            6   2147483647    2147483647   2147483647            3            0            4   2147483647   2147483647    2147483647   2147483647            5            4            0            2            8            16            7            6   2147483647            2            0            9            14   2147483647   2147483647   2147483647            8            9            0  排序前： [Edge <A--B>=12, Edge <A--F>=16, Edge <A--G>=14, Edge <B--C>=10, Edge <B--F>=7, Edge <C--D>=3, Edge <C--E>=5, Edge <C--F>=6, Edge <D--E>=4, Edge <E--F>=2, Edge <E--G>=8, Edge <F--G>=9] 排序后： [Edge <E--F>=2, Edge <C--D>=3, Edge <D--E>=4, Edge <C--E>=5, Edge <C--F>=6, Edge <B--F>=7, Edge <E--G>=8, Edge <F--G>=9, Edge <B--C>=10, Edge <A--B>=12, Edge <A--G>=14, Edge <A--F>=16] 克鲁斯卡尔最小生成树结果:[Edge <E--F>=2, Edge <C--D>=3, Edge <D--E>=4, Edge <B--F>=7, Edge <E--G>=8, Edge <A--B>=12] 

迪杰斯特拉算法

基本介绍

• 迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个结点到其他结点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

算法过程

设置出发顶点为v，顶点集合V{v1,v2,vi…}，v到V中各顶点的距离构成距离集合Dis，Dis{d1,d2,di…}，Dis集合记录着v到图中各顶点的距离(到自身可以看作0，v到vi距离对应为di)。

• 从Dis中选择值最小的di并移出Dis集合，同时移出V集合中对应的顶点vi，此时的v到vi即为最短路径。
• 更新Dis集合，更新规则为：比较v到V集合中顶点的距离值，与v通过vi到V集合中顶点的距离值，保留值较小的一个(同时也应该更新顶点的前驱节点为vi，表明是通过vi到达的)。
• 重复执行两步骤，直到最短路径顶点为目标顶点即可结束。

最佳实践-最短路径

需求

• 战争时期，胜利乡有7个村庄(A, B, C, D, E, F, G) ，现在有六个邮差，从G点出发，需要分别把邮件分别送到 A, B, C , D, E, F 六个村庄，各个村庄的距离用边线表示(权) ，比如 A – B 距离 5公里。
• 问：如何计算出G村庄到 其它各个村庄的最短距离?
• 如果从其它点出发到各个点的最短距离又是多少?
  

思路分析

代码实现

public class DijkstraCase { /**      * 定义图      */ static class Graph { char[] vertices; int[][] matrix;         VisitedVertex vv; Graph(char[] vertices, int[][] matrix) { this.vertices = vertices; this.matrix = matrix; } void show() {             System.out.println("邻接矩阵："); for (int[] arr : matrix) { for (int a : arr) {                     System.out.printf("%12dt", a); }                 System.out.println(); } } /**          * 迪杰斯特拉算法实现          *          * @param index 出发顶点的索引下标          */ void dsj(int index) {             System.out.printf("==>> 从顶点%s出发到各个顶点的最短路径情况：n", vertices[index]);             vv = new VisitedVertex(vertices.length, index); // 更新 index 顶点到周围顶点的距离和前驱顶点 update(index); for (int j = 1; j < vertices.length; j++) { // 选择并返回新的访问顶点                 index = vv.updateArr(); update(index); } // 显示结果             vv.show(); // 最短距离 int count = 0; for (int i : vv.dis) { if (i != M) {                     System.out.print(vertices[count] + "(" + i + ")"); } else {                     System.out.println("N "); }                 count++; }             System.out.println(); } /**          * 更新index下标顶点到周围顶点的距离和周围顶点的前驱结点          */ void update(int index) { int len; for (int j = 0; j < matrix[index].length; j++) { // len含义：出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和                 len = vv.getDis(index) + matrix[index][j]; // 如果j顶点没有被访问过，并且len小于出发顶点到j顶点的距离，就需要更新 if (!vv.in(j) && len < vv.getDis(j)) { // 更新 j 顶点的前驱为 index 顶点                     vv.updatePre(j, index); // 更新出发顶点到 j 顶点的距离                     vv.updateDis(j, len); } } } } static class VisitedVertex { /**          * 记录各个顶点是否访问过 1 表示访问过,0 未访问,会动态更新          */ int[] alreadyArr; /**          * 每个下标对应的值为前一个顶点下标, 会动态更新          */ int[] preVisited; /**          * 记录出发顶点到其他所有顶点的距离,比如 G 为出发顶点，就会记录 G 到其它顶点的距离，会动态更新，求          * 的最短距离就会存放到 dis          */ int[] dis; /**          * @param length 表示顶点的个数          * @param index  出发顶点对应的下标，比如G，下标为6          */ VisitedVertex(int length, int index) { this.alreadyArr = new int[length]; this.preVisited = new int[length]; this.dis = new int[length]; // 初始化dis             Arrays.fill(dis, M); // 设置出发顶点被访问 this.alreadyArr[index] = 1; // 设置出发顶点的访问距离为0 this.dis[index] = 0; } /**          * 判断index顶点是否被访问过          */ boolean in(int index) { return alreadyArr[index] == 1; } /**          * 更新出发顶点到index顶点的距离          */ void updateDis(int index, int len) {             dis[index] = len; } /**          * 更新pre这个顶点的前驱顶点为index顶点          */ void updatePre(int pre, int index) {             preVisited[pre] = index; } /**          * 返回出发顶点到index的距离          */ int getDis(int index) { return dis[index]; } /**          * 继续选择并返回新的访问顶点，比如这里的G完成后，就是A作为新的访问顶点(不是出发顶点)          */ int updateArr() { int min = M, index = 0; for (int i = 0; i < alreadyArr.length; i++) { if (alreadyArr[i] == 0 && dis[i] < min) {                     min = dis[i];                     index = i; } } // 更新index顶点被访问             alreadyArr[index] = 1; return index; } /**          * 显示访问结果，即三个数组的情况          */ void show() {             System.out.println("alreadyArr = " + Arrays.toString(alreadyArr));             System.out.println("preVisited = " + Arrays.toString(preVisited));             System.out.println("dis = " + Arrays.toString(dis)); } } private static final int M = 65535; public static void main(String[] args) { char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; int[][] matrix = { {M, 5, 7, M, M, M, 2}, {5, M, M, 9, M, M, 3}, {7, M, M, M, 8, M, M}, {M, 9, M, M, M, 4, M}, {M, M, 8, M, M, 5, 4}, {M, M, M, 4, 5, M, 6}, {2, 3, M, M, 4, 6, M}, }; // 创建图对象         Graph graph = new Graph(vertices, matrix); // 打印图         graph.show();          graph.dsj(6);         graph.dsj(2); } } 

• 结果输出：

邻接矩阵：        65535            5            7        65535        65535        65535            2             5        65535        65535            9        65535        65535            3             7        65535        65535        65535            8        65535        65535         65535            9        65535        65535        65535            4        65535         65535        65535            8        65535        65535            5            4         65535        65535        65535            4            5        65535            6             2            3        65535        65535            4            6        65535  ==>> 从顶点G出发的最短路径情况： alreadyArr = [1, 1, 1, 1, 1, 1, 1] preVisited = [6, 6, 0, 5, 6, 6, 0] dis = [2, 3, 9, 10, 4, 6, 0] A(2)B(3)C(9)D(10)E(4)F(6)G(0) ==>> 从顶点C出发的最短路径情况： alreadyArr = [1, 1, 1, 1, 1, 1, 1] preVisited = [2, 0, 0, 5, 2, 4, 0] dis = [7, 12, 0, 17, 8, 13, 9] A(7)B(12)C(0)D(17)E(8)F(13)G(9) 

弗洛伊德算法

基本介绍

• 和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
• 弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径。
• 迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。
• 弗洛伊德算法 VS 迪杰斯特拉算法：迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他顶点的最短路径；弗洛伊德算法中每一个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每一个顶点到其他顶点的最短路径。

算法分析

• 设置顶点vi到顶点vk的最短路径已知为Lik，顶点vk到vj的最短路径已知为Lkj，顶点vi到vj的路径为Lij，则vi到vj的最短路径为：min((Lik+Lkj),Lij)，vk的取值为图中所有顶点，则可获得vi到vj的最短路径。
• 至于vi到vk的最短路径Lik或者vk到vj的最短路径Lkj，是以同样的方式获得。
• 弗洛伊德(Floyd)算法图解分析-举例说明：

最佳实践-最短路径

需求

• 胜利乡有7个村庄(A, B, C, D, E, F, G)，各个村庄的距离用边线表示(权) ，比如 A – B 距离 5公里，问：如何计算出各村庄到 其它各村庄的最短距离?
  

算法图解

• 第一轮循环中，以A(下标为：0)作为中间顶点，距离表和前驱关系更新为：
  
• 分析如下：
• ① 以A顶点作为中间顶点是，B->A->C的距离由N->9，同理C到B；C->A->G的距离由N->12，同理G到C。
• ② 更换中间顶点，循环执行操作，直到所有顶点都作为中间顶点更新后，计算结束。
  

代码实现

public class FloydCase { /**      * 定义图      */ static class Graph { /**          * 顶点数组          */ char[] vertices; /**          * 记录各个顶点出发到其它各个顶点的距离，最后的结果也是保留在该数组中          */ int[][] dis; /**          * 保存到达目标顶点的前驱顶点          */ int[][] pre; Graph(char[] vertices, int[][] matrix) { this.vertices = vertices; this.dis = matrix; int len = vertices.length; this.pre = new int[len][len]; // 对数组pre初始化 for (int i = 0; i < len; i++) {                 Arrays.fill(pre[i], i); } } /**          * 显示pre和dis          */ void show() { for (int k = 0; k < dis.length; k++) { // 输出pre的一行数据 for (int i = 0; i < dis.length; i++) {                     System.out.printf("%8st", vertices[pre[k][i]]); }                 System.out.println(); // 输出dis的一行数据 for (int i = 0; i < dis.length; i++) {                     System.out.printf("%8st", String.format("%s->%s(%s)", vertices[k], vertices[i], dis[k][i] == N ? "N" : dis[k][i])); }                 System.out.println();                 System.out.println(); } } /**          * 弗洛伊德算法实现          */ void floyd() { // 保存距离 int len = 0; // 对中间顶点进行遍历，k就是中间顶点的索引下标 for (int k = 0; k < dis.length; k++) { // 从i顶点出发[A, B, C, D, E, F, G] for (int i = 0; i < dis.length; i++) { for (int j = 0; j < dis.length; j++) {                         len = dis[i][k] + dis[k][j]; if (len < dis[i][j]) { // 更新距离                             dis[i][j] = len; // 更新前驱结点                             pre[i][j] = pre[k][j]; } } } }             System.out.println("==>> 弗洛伊德算法求图的各个顶点的到其它顶点的最短路径输出："); show(); } } private static final int N = 65535; public static void main(String[] args) { char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; int[][] matrix = { {0, 5, 7, N, N, N, 2}, {5, 0, N, 9, N, N, 3}, {7, N, 0, N, 8, N, N}, {N, 9, N, 0, N, 4, N}, {N, N, 8, N, 0, 5, 4}, {N, N, N, 4, 5, 0, 6}, {2, 3, N, N, 4, 6, 0}, };         Graph graph = new Graph(vertices, matrix);         System.out.println("初始情况：");         graph.show();          graph.floyd(); } } 

• 结果输出：

初始情况：        A        A        A        A        A        A        A   A->A(0)  A->B(5)  A->C(7)  A->D(N)  A->E(N)  A->F(N)  A->G(2)          B        B        B        B        B        B        B   B->A(5)  B->B(0)  B->C(N)  B->D(9)  B->E(N)  B->F(N)  B->G(3)          C        C        C        C        C        C        C   C->A(7)  C->B(N)  C->C(0)  C->D(N)  C->E(8)  C->F(N)  C->G(N)          D        D        D        D        D        D        D   D->A(N)  D->B(9)  D->C(N)  D->D(0)  D->E(N)  D->F(4)  D->G(N)          E        E        E        E        E        E        E   E->A(N)  E->B(N)  E->C(8)  E->D(N)  E->E(0)  E->F(5)  E->G(4)          F        F        F        F        F        F        F   F->A(N)  F->B(N)  F->C(N)  F->D(4)  F->E(5)  F->F(0)  F->G(6)          G        G        G        G        G        G        G   G->A(2)  G->B(3)  G->C(N)  G->D(N)  G->E(4)  G->F(6)  G->G(0)   ==>> 弗洛伊德算法求图的各个顶点的到其它顶点的最短路径输出：        A        A        A        F        G        G        A   A->A(0)  A->B(5)  A->C(7) A->D(12)  A->E(6)  A->F(8)  A->G(2)          B        B        A        B        G        G        B   B->A(5)  B->B(0) B->C(12)  B->D(9)  B->E(7)  B->F(9)  B->G(3)          C        A        C        F        C        E        A   C->A(7) C->B(12)  C->C(0) C->D(17)  C->E(8) C->F(13)  C->G(9)          G        D        E        D        F        D        F  D->A(12)  D->B(9) D->C(17)  D->D(0)  D->E(9)  D->F(4) D->G(10)          G        G        E        F        E        E        E   E->A(6)  E->B(7)  E->C(8)  E->D(9)  E->E(0)  E->F(5)  E->G(4)          G        G        E        F        F        F        F   F->A(8)  F->B(9) F->C(13)  F->D(4)  F->E(5)  F->F(0)  F->G(6)          G        G        A        F        G        G        G   G->A(2)  G->B(3)  G->C(9) G->D(10)  G->E(4)  G->F(6)  G->G(0) 

马踏棋盘算法

基本介绍

• 马踏棋盘算法也被称为骑士周游问题，将马随机放在国际象棋的8×8棋盘Board[0～7][0～7]的某个方格中，马按走棋规则(马走日字)进行移动。要求每个方格只进入一次，走遍棋盘上全部64个方格。
• 游戏演示：添加链接描述
  

最佳实践-马踏棋盘

思路分析

• 马踏棋盘问题(骑士周游问题)实际上是图的深度优先搜索(DFS)的应用。
• 如果使用回溯（就是深度优先搜索）来解决，假如马儿踏了53个点，如图：走到了第53个，坐标（1,0），发现已经走到尽头，没办法，那就只能回退了，查看其他的路径，就在棋盘上不停的回溯…… ，思路分析+代码实现。
• 分析第一种方式的问题，并使用贪心算法（greedyalgorithm）进行优化，解决马踏棋盘问题。
• 使用前面的游戏来验证算法是否正确。
  

代码实现

public class HorseChessboard { /**      * 棋盘的行数和列数      */ private static int X; private static int Y; /**      * 创建一个数组，标记棋盘的各个位置是否被访问过      */ private static boolean[] visited; /**      * 使用一个属性，标记是否棋盘的所有位置都被访问      * 如果为 true,表示成功      */ private static boolean finished; public static void main(String[] args) {         X = 8;         Y = 8;         System.out.printf("骑士周游[%d * %d]算法，开始运行~~n", X, Y); // 马儿初始位置的行、列 int row = 0, column = 0; // 创建棋盘 int[][] chessboard = new int[X][Y]; // 初始值都是 false         visited = new boolean[X * Y]; long startTime = System.currentTimeMillis(); traversalChessboard(chessboard, row, column, 1); long endTime = System.currentTimeMillis();          System.out.println("共耗时: " + (endTime - startTime) + " 毫秒"); //输出棋盘的最后情况 for (int[] rows : chessboard) { for (int step : rows) {                 System.out.print(step + "t"); }             System.out.println(); } } private static void traversalChessboard(int[][] chessboard, int row, int column, int step) {         chessboard[row][column] = step; // 标记已访问         visited[row * X + column] = true; // 获取当前位置可以走的下一个位置的集合         List<Point> points = next(new Point(column, row)); // 对 points 进行排序，排序的规则就是对 points 的所有的 Point 对象的下一步的位置的数目，进行非递减排序 sort(points); // 遍历points while (points.size() > 0) { // 取出下一个可以走的位置             Point p = points.remove(0); // 判断是否访问过 if (!visited[p.y * X + p.x]) { traversalChessboard(chessboard, p.y, p.x, step + 1); } } // 判断马儿是否完成了任务，使用 step 和应该走的步数比较，如果没有达到数量，则表示没有完成任务，将整个棋盘置 0 // 说明: step < X * Y 成立的情况有两种:1、棋盘到目前位置,仍然没有走完，2、棋盘处于一个回溯过程 if (step < X * Y && !finished) {             chessboard[row][column] = 0;             visited[row * X + column] = false; } else {             finished = true; } } private static List<Point> next(Point curPoint) {         List<Point> points = new ArrayList<>();         Point p = new Point(); /*0*/ if ((p.x = curPoint.x + 2) < X && (p.y = curPoint.y - 1) >= 0) points.add(new Point(p)); /*1*/ if ((p.x = curPoint.x + 2) < X && (p.y = curPoint.y + 1) < Y) points.add(new Point(p)); /*2*/ if ((p.x = curPoint.x + 1) < X && (p.y = curPoint.y + 2) < Y) points.add(new Point(p)); /*3*/ if ((p.x = curPoint.x - 1) >= 0 && (p.y = curPoint.y + 2) < Y) points.add(new Point(p)); /*4*/ if ((p.x = curPoint.x - 2) >= 0 && (p.y = curPoint.y + 1) < Y) points.add(new Point(p)); /*5*/ if ((p.x = curPoint.x - 2) >= 0 && (p.y = curPoint.y - 1) >= 0) points.add(new Point(p)); /*6*/ if ((p.x = curPoint.x - 1) >= 0 && (p.y = curPoint.y - 2) >= 0) points.add(new Point(p)); /*7*/ if ((p.x = curPoint.x + 1) < X && (p.y = curPoint.y - 2) >= 0) points.add(new Point(p)); return points; } /**      * 根据当前这一步的所有的下一步的选择位置，进行非递减排序, 减少回溯的次数      */ private static void sort(List<Point> points) {         points.sort((p1, p2) -> { //获取到 p1 的下一步的所有位置个数 int count1 = next(p1).size(); //获取到 p2 的下一步的所有位置个数 int count2 = next(p2).size(); if (count1 < count2) { return -1; } else if (count1 == count2) { return 0; } else { return 1; } }); } } 

• 结果输出：

骑士周游[8 * 8]算法，开始运行~~ 共耗时: 52 毫秒 1 16 43 32 3 18 45 22  42 31 2 17 44 21 4 19  15 56 53 60 33 64 23 46  30 41 58 63 54 61 20 5  57 14 55 52 59 34 47 24  40 29 38 35 62 51 6 9  13 36 27 50 11 8 25 48  28 39 12 37 26 49 10 7 

卖油翁和老黄牛

卖油翁的故事

老黄牛精神