SAT问题:给定一个命题公式 SAT求解能力的发展: SAT求解器的输入一般是CNF,这里为便于讨论,引入关于CNF的集合表示。 一个公式(formula)可以视为子句(clause)的集合: 一些方便的表达方式: 在这种符号体系下,会有以下命题成立(有点绕,需要多看几遍): 只有一条规则: 解决较大规模问题的效率低下 大致思路:从一个空的解释(interpretation)出发,每次扩展一个变量的取值 在实现策略上更加灵活 举例: 通俗的说,就是深度优先搜索。在某些算法中优化了回退策略。 基础的回退规则比较“笨”: DPLL见DPLL
程序验证(二):SAT问题
概念:Satisfiability Problem
F,决定是否存在一个解释
I使得
I⊨F.
3SAT问题是首个被确定的NP完全问题。
大多数重要逻辑问题可以归约为SAT:
关键:将搜索与推理结合以提高效率CNF详解
集合表示
C1∧...∧Cn
可以表示为:
{C1,...,Cn}
同样,子句可以视为文字(literal)的集合:
(P∨Q)∧(Q→¬P)
可以表示为:
{{P,Q},{¬Q,¬P}}
一些通用的表示方法:
F
C
P,Q,R,...
Ci{P↦F}: 在子句
Ci中使用
F替代
P
Ci[P]: 变量
P在子句
Ci中是不取非的,也就是
Ci={...,P,...}
Ci[¬P]: 变量
P在
Ci中是取非的,也就是
Ci={...,¬P,...}
以
F表示公式,
C表示子句,基于CNF公式的集合表示,有:
Ci∨Cj: union of
Ci and
Cj,
Ci∪Cj
Fi∧Fj: union of
Fi and
Fj,
Fi∪Fj归结(resolution)
C1{P↦⊥}∨C2{¬P↦⊥}C1[P] C2[¬P]
给定两个具有相同变量
P,但是对于
P取非情况不同的两个子句,那么:
P为真,那么
C2中的其它文字必然为真
P为假,那么
C1中的其它文字必然为假
P,也就是归结
C1{P↦⊥}∨C2{¬P↦⊥}叫做归结式(resolvent)
这个归结式可以作为一个合取子句加入到原公式,这样得到的新公式与原公式等价。
而如果
C1{p↦⊥}∨C2{¬P↦⊥}=⊥∨⊥=⊥:
C1∧C2是不可满足的
{C1,C2}在内的CNF都是不可满足的
举例:
A∨B∨C与
¬A∨B∨D的归结子句是
B∨C∨D归结法求解SAT
归结算法
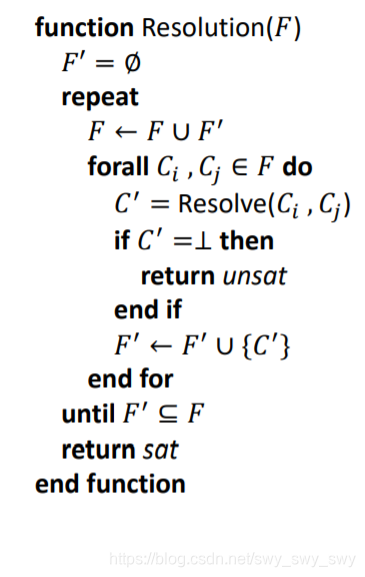
F′是所有归结式的集合
F以包含以产生的归结式
F上重复归结过程
⊥归结式 2.无法再更新
F(此时所有的可归结的子句都已经被归结了)
举例:
(P∨Q)∧(P→R)∧(Q→R)∧¬R
步骤
子句
备注
1
p∧Q–
2
¬P∨R–
3
¬Q∨R–
4
¬R–
5
Q∨R1&2
6
R3&5
7
⊥4&6
归结算法的评价
基于搜索的方法
部分解释
如果
I是一个部分解释,文字
ℓ可以为
true,
false,
undef:
true(satisfied):
I⊨ℓ
false(conflicting):
I⊨ℓ
undef:
var(ℓ)∈I
给定一个子句
C和解释
I:
true under
I iff
I⊨C
false under
I iff
I⊨C
unit under
I iff
C=C′∨ℓ,I⊨C′,
ℓ is
undef
undefiff: if and only if,当且仅当 unit: 单元,一个新引入的概念
令
I={P1↦1,P2↦0,P4↦1},那么有:
P1∨P3∨¬P4 is
true
¬P1∨P2 is
false
¬P1∨¬P4∨P3 is
unit
¬P1∨P3∨P5 is
undef搜索程序:一个状态机
程序的状态包括:
sat
unsat
[I]∥F, 这里的
[I]是一个解释,
F是一个CNF
初始状态:
[Φ]∥F
结束状态:
sat,
unsat
中间状态:
[Φ]∥F1,
C: 解释为空,
F=F1∧C
[I1,Pˉ,I2]∥F: 解释先置为
I1,然后
P↦0, 然后解释为
I2搜索规则
[I]∥F↪[I,P∘]∥F if{P occurs in FP unassigned in I
[I1,P∘,I2]∥F↪[I1,Pˉ]∥F if{[I1,P,I2]⊨FP last decision in interp.
[I]∥F↪sat if [I]⊨F
[I]∥F↪unsat if{I⊨FNo decisions in I
以上四条规则足以构建一个基本的sat求解器
我们可以进一步优化。比如在
unit子句中,对于解释
I与子句
C,有
I不满足
C
C中有且只有一个文字被置为假
那么根据归结原理,有:
[I]∥F,C∨P↪[I,P]∥F,C∨P
[I]∥F,C∨¬P↪[I,Pˉ]∥F,C∨¬P
条件是
I⊨C,and P undefined in I高级回退&子句学习
引入回跳规则(BackJump Rule):
[I1,P∘,I2]∥F↪[I1,ℓ]∥F,(C→l) if⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧[I1,P∘,I2]⊨FExists C s.t.:F⇒(C→l)I1⊨Cvar(ℓ) undef. in I1var(ℓ) appears in F
这里
C→l就叫做冲突子句,我们只要避免冲突子句就可以进一步寻找解。
那么,如何找到冲突子句呢?
构造一个蕴含图(implication graph)
G=(V,E):
V对于解释
I中每一个判定文字都有一个节点,用这个文字的值和它的判定等级来标记(说白了就是这个文字是你所判定的第几个文字)
C=ℓ1∨...∨ℓn∨ℓ,其中
ℓ1,...,ℓn被赋值为假,首先为
ℓ添加一个节点,它的判定等级就是它进入到
I的顺序,然后添加边
(ℓi,ℓ)到
E,其中
1≤i≤n
Λ。对于所有标记为
P与
¬P的冲突变元,在
E中添加从这些节点到
Λ的边。
例如:
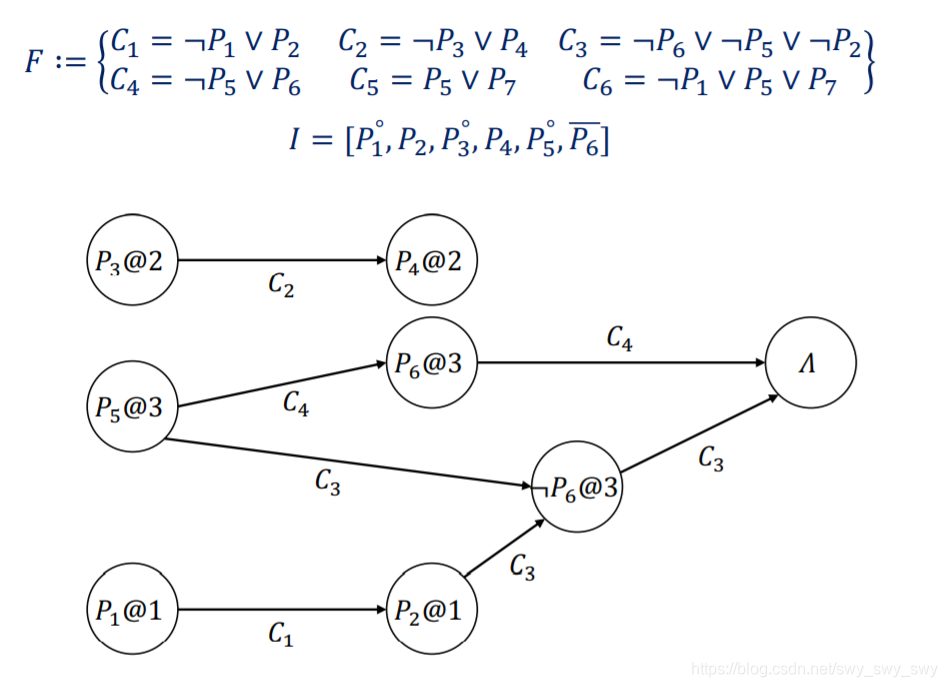
冲突图:只有一个冲突变元,且所有节点都具有通往
Λ的路径的蕴含图
例如:
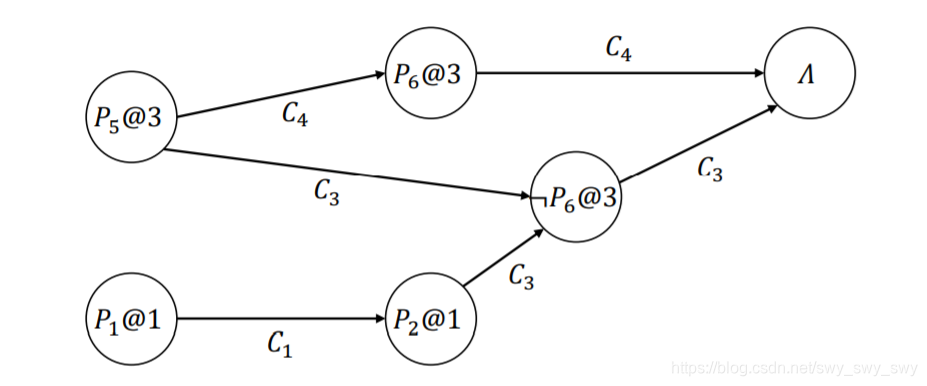
获得冲突子句:
考虑一个冲突图
G
G中切一刀,使得:
K
K中的节点即为冲突的原因
例如:
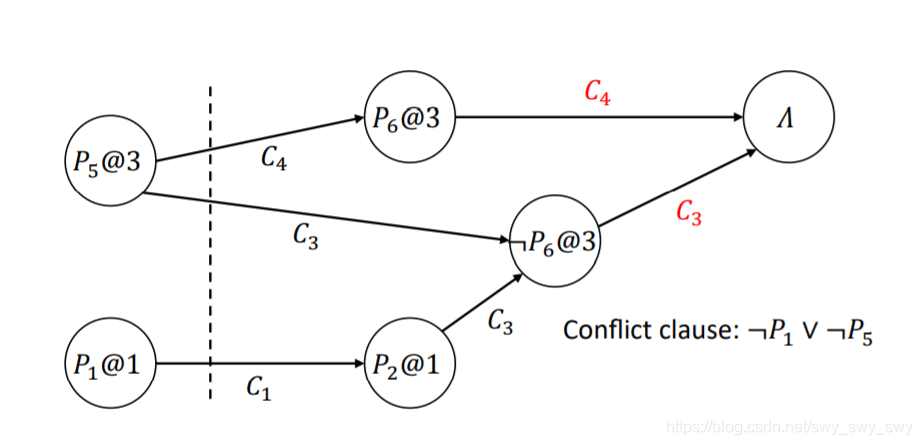
图中,
¬P5∨¬P2和
¬P5∨P6可以作为冲突子句DPLL & CDCL
CDCL即为(Conflict-Driven Clause Learning),是目前SAT求解器主要采用的方法。
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)