其实八大排序如果弄清楚它们的原理并不难,虽然里面有几种排序写起来也很麻烦。 每种排序都有相对应的解释和图,大家可以看完解释和图然后按照自己的思路去写代码。(当然也提供了测试好的代码) 末尾提供了测试代码,你只需要改动一行代码,就可以测试你的排序是否正确,如果错误会打印出原本序列、你的排序、正确的排序,以帮助你更好的排错。
稳定性:如果一组待排序的数字中,有两个相同的数字。在完成排序后,这两个数字的相对位置不变,即该排序是稳定排序。 不稳定的排序算法:堆排序、快速排序、希尔排序、直接选择排序. 0(nlogn) 快速排序、堆排序、归并排序,快速排序最好 初始顺序对排序没有影响的是 堆排序 循环遍历 0-length-1 的元素,找到最合适每个位置的元素。 每次选择一个数作为标准,然后比它大的放在右边,比它小的放在左边。 注: 我们从 1 开始遍历每一个元素(i),然后把元素 i 插入到 0-i 里面最合适的位置,这样就排好序了。 希尔排序其实是直接插入排序的一个改进。 直接插入排序每次移动的步长都是 1 ,而希尔排序的步长从 size 开始 直到 1,这样做的使得 大的数字比较靠后,小的数字比较靠前。 当进行步长为 1 的直接插入排序的时候,就不会出现每次移动很多的情况。 先将整个待排序列分割成若干个子序列,对每个子序列进行直接插入排序,等到整个序列基本有序的时候,在进行一次整体的直接插入排序(也就是 步长为 1)。 每次从i – length-1中选择出 一个最小(最大)的数字,然后和 i 进行交换。 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i4WCqdFO-1590475243176)( 把待排序列变成最大堆(最小堆),然后取出对顶元素。重复以上操作,直到排序结束。 把序列尽可能的等分,然后两半分别排序。排序好后再合并排序 基数排序要根据具体的序列规则来做,这里以最简单的十位数为例,作图。 因为基数排序和具体的序列有关,这里以最简单的个位数为例,方便你阅读代码。 你可以使用下面的工具类,对你写的排序方法进行测试。 关注我吧,一个喜欢胡思乱想的程序员。
但是最难的往往就是,我们会把它们相互混淆,我给每个排序画了一张动图,看图记忆就好很多了。 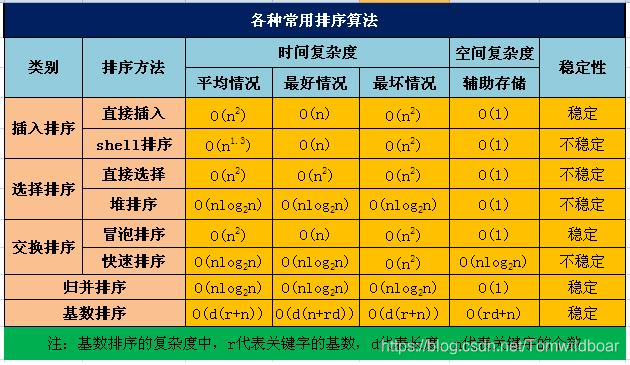
一、冒泡排序
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
类别
O(n2)
O(n)
O(n2)
O(1)
稳定
交换排序
1-1:冒泡排序的解释
把位置 i 的元素和i后面的的每个元素对比,找到最小的元素放在 i 这个位置。(找最大还是最小取决你怎么排序)
下面是图示:
1-2:冒泡排序代码
public void bubbleSort(int[] arr){ int tmp; for (int i = 0;i < arr.length - 1; i++){ for (int j = i+1; j < arr.length; j++){ if (arr[i] > arr[j]){ tmp = arr[j]; arr[j] = arr[i]; arr[i] = tmp; } } } } 二、快速排序
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
类别
O(nlog2n)
O(nlog2n)
O(n2)
O(nlog2n)
不稳定
交换排序
2-1:快速排序的解释
通过上面的操作把数组分成了两份,然后每份继续重复这样的操作,直到排序好。
1、为了方便,这个标准数,我们每次取第一个数
2、当左边长度是1的时候就是排序好了。(同理右边也是)
2-2:快速排序代码
public static void quickSort(int[] arr,int left, int right){ int tmpLeft = left; int tmpRight = right; int cur = arr[left]; while (left < right){ while (arr[right] >= cur && right > left) { right--; } arr[left] = arr[right]; while (arr[left] < cur && right > left) { left ++; } arr[right] = arr[left]; } arr[left] = cur; if (left - tmpLeft > 1){ quickSort(arr,tmpLeft,left-1); } if (tmpRight - left > 0){ quickSort(arr,left+1,tmpRight); } } 三、直接插入排序
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
类别
O(n2)
O(n)
O(n2)
O(1)
稳定
插入排序
3-1:直接插入排序的解释
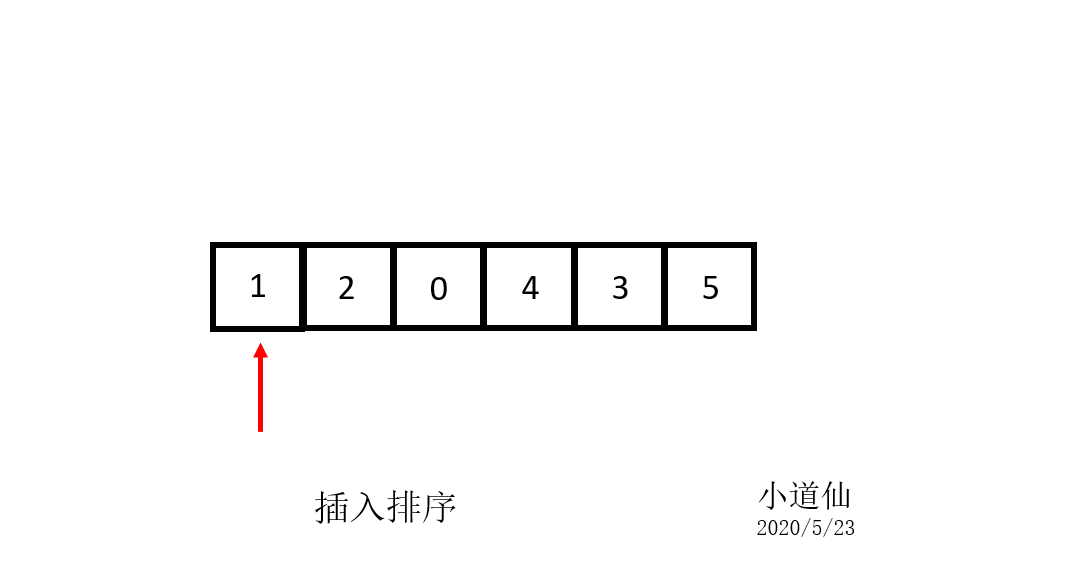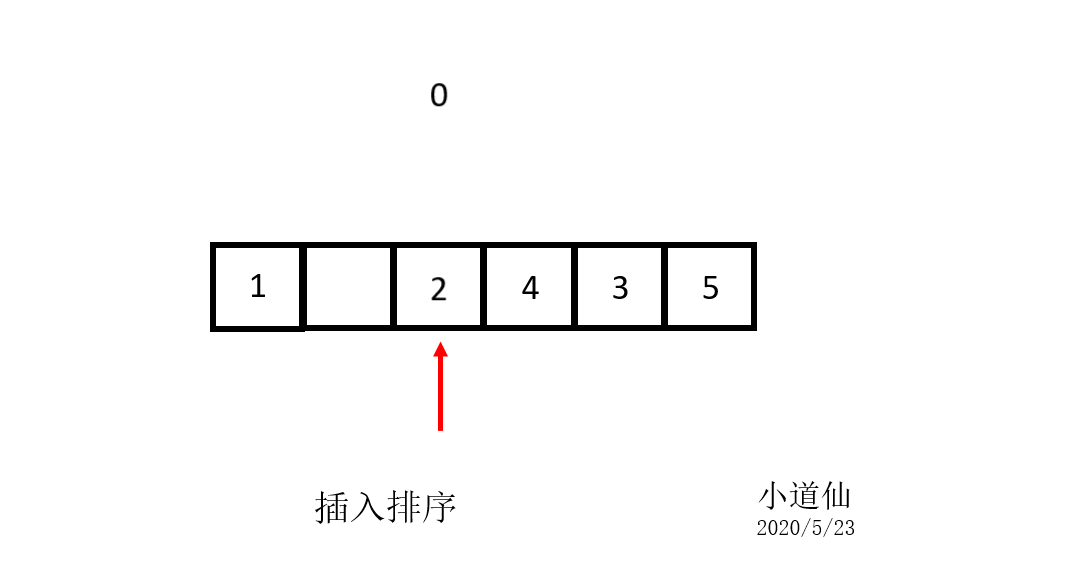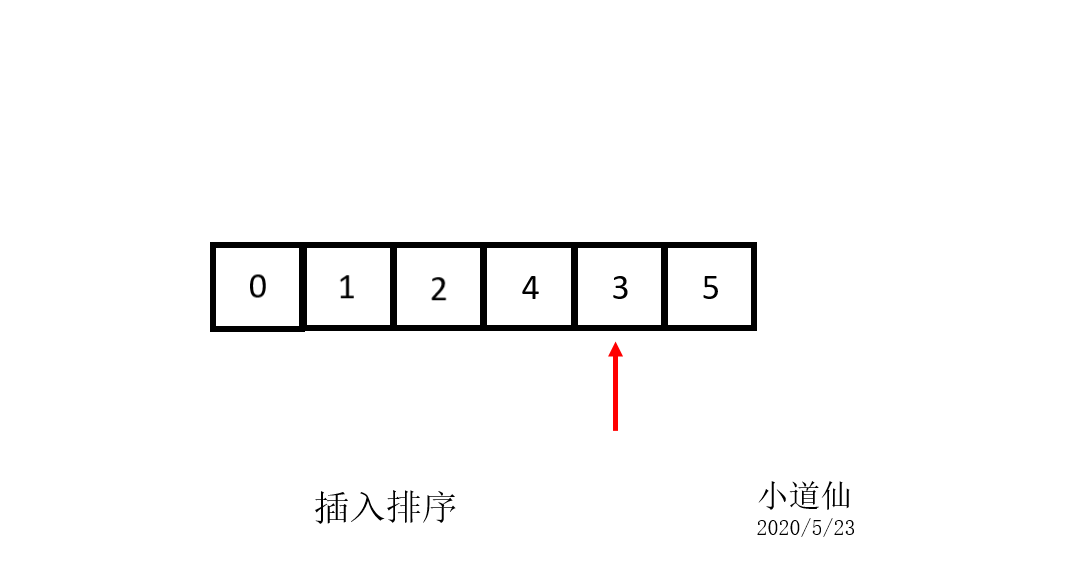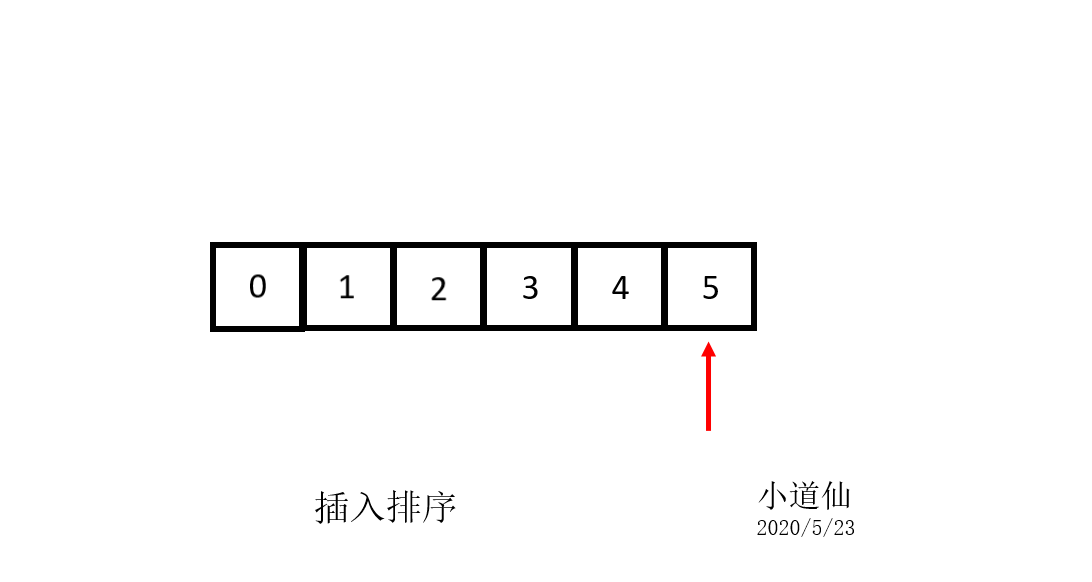
3-2:直接插入排序的代码
public void insertSort(int[] arr){ int tmp,j; for (int i = 1;i < arr.length; i++){ if (arr[i] < arr[i-1]){ tmp = arr[i]; for (j = i;j > 0; j--){ if (tmp < arr[j-1]){ arr[j] = arr[j-1]; }else { break; } } arr[j] = tmp; } } } 四、希尔排序
4-1:希尔排序解释
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
类别
O(n1.3)
O(n)
O(n2)
O(1)
不稳定
交换排序
public void shellInsert(int[] arr, int step){ int tmp; int m; for (int i = 0; i < step; i++){ for (int n = i + step;n < arr.length; n += step){ if (arr[n] < arr[n - step]){ tmp = arr[n]; for (m = n-step;m >= 0; m -= step){ if (tmp < arr[m]){ arr[m + step] = arr[m]; }else { break; } } arr[m+step] = tmp; } } } } public void shellSort(int[] arr){ int step = arr.length / 2; // int step = 1; while (step >= 1){ shellInsert(arr, step); step = step / 2; } } 五、直接选择排序
5-1:直接选择排序解释
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
类别
O(n2)
O(n2)
O(n2)
O(1)
不稳定
选择排序
5-2:直接选择排序代码
public void selectSort(int[] arr){ int min_i,tmp; for (int i = 0;i < arr.length - 1; i++){ min_i = i; for (int j = i+1;j < arr.length; j++){ if (arr[min_i] > arr[j]){ min_i = j; } } tmp = arr[i]; arr[i] = arr[min_i]; arr[min_i] = tmp; } } 六、堆排序
6-1:堆排序解释
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
类别
O(nlog2n)
O(nlog2n)
O(nlog2n)
O(1)
不稳定
选择排序
最大堆你可以把它看成二叉树,根元素,大于左右节点。
6-2:堆排序代码
//当列表第一个是以下标0开始,结点下标为i,左孩子则为2*i+1,右孩子下标则为2*i+2,若下标以1开始,左孩子则为2*i,右孩子则为2*i+1 public static void heapAdjust(int a[], int s, int m){ int key = a[s]; for(int j = 2*s + 1; j <= m; j = 2*j + 1 ){ // 找到左节点和右节点中小的节点 if(j < m && a[j] <= a[j+1] ) { ++j; } // 如果当前值比左右节点最小值还小就不用管了 if( a[j] <= key ){ break; } a[s] = a[j]; s = j; } a[s] = key; } public static void heap_sort(int a[], int size){ //初始建堆,从最后一个非叶子节点开始 for(int i = size/2-1; i >= 0; --i){ heapAdjust(a, i, size-1); } //取堆顶,并且调整 int tmp; for(int i = size-1; i > 0 ; --i){ tmp = a[0]; a[0] = a[i]; a[i] = tmp; heapAdjust(a, 0, i-1); } } 七、归并排序
7-1:归并排序的解释
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
O(nlog2n)
O(nlog2n)
O(nlog2n)
O(n)
稳定
7-2:归并排序代码
/** * 每个部分进行排序 */ public void sort(int[] arr,int i,int mid,int j){ int[] brr = new int[j-i+1]; int start_one = i; int start_two = mid+1; int cur = 0; while (start_one <= mid && start_two <= j){ brr[cur ++] = arr[start_one] < arr[start_two] ? arr[start_one ++] : arr[start_two ++]; } while (start_one <= mid){ brr[cur ++] = arr[start_one++]; } while (start_two <= j){ brr[cur ++] = arr[start_two++]; } for (int k = 0;k < cur; k++){ arr[i ++] = brr[k]; } } /** * 拆分成一个个部分 */ public void mergeSort(int[] arr,int i,int j){ if (i >= j) return; int mid = (i + j) / 2; mergeSort(arr, i, mid); mergeSort(arr,mid + 1, j); sort(arr, i,mid,j); } 八、基数排序
8-1:基数排序的解释
平均时间复杂度
最好时间复杂度
最坏时间复杂度
空间复杂度
稳定性
O(d(r+n))
O(d(n+rd))
O(nlog2n)
O(n)
稳定
先以个位数进行排序,然后再以10位数进行排序。回收的结果就是排序好的结果。
8-2:基数排序代码
public static void radixSort(int[] arr){ // 创建0-9的桶 List<List<Integer>> lists = new ArrayList<>(); for (int i = 0;i < 10; i++){ lists.add(new ArrayList<>()); } // 按照顺序把数字装入桶中 for (int j = 0;j < arr.length; j++){ lists.get(arr[j]).add(arr[j]); } // 按照顺序回收桶中的数据 int cur = 0; for (List<Integer> item : lists){ for (Integer i : item){ arr[cur ++] = i; } } } 测试代码
/** * 测试排序规则 * 1、测试100次,每次随机出现0-100的数字 * 2、arr 使用系统的排序, brr我们自己的排序, crr 不排序 * 3、对比arr 和 brr看是否相同,如不相同就打印 arr、brr 、crr * 4、你每次只需要替换下面注释地 * * @author 小道仙 * @date 2020年5月23日 */ public static boolean testSort(){ int arrayLenght = 100; int[] arr = new int[arrayLenght]; int[] brr = new int[arrayLenght]; int[] crr = new int[arrayLenght]; int tmp,cur; for (int i = 0;i < 10000; i++){ cur = 0; for (int j = 0; j < arrayLenght; j++){ tmp = (int)(Math.random()*100); arr[cur] = tmp; crr[cur] = tmp; brr[cur ++] = tmp; } Arrays.sort(arr); try { // 每次测试替换掉下面的这个排序方法 // heap_sort(brr, brr.length); }catch (Exception e){ e.printStackTrace(); } for (int k = 0;k < cur; k++){ if (arr[k] != brr[k]){ print(arr,brr,crr); return false; } } } return true; } private static void print(int[] arr,int[] brr,int[] crr){ System.out.print("arr : "); for (int i = 0;i < arr.length; i++){ System.out.print(arr[i] + " "); } System.out.println(); System.out.print("brr : "); for (int i = 0;i < brr.length; i++){ System.out.print(brr[i] + " "); } System.out.println(); System.out.print("crr : "); for (int i = 0;i < crr.length; i++){ System.out.print(crr[i] + " "); } System.out.println(); System.out.println(); } 
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)