如果觉得这个文章有用的话,何不评论支持一下新人哦! 上一篇文章 从入门角度深入理解——有关最短路的常见算法#1 最短路问题介绍。 简单介绍了图的基本知识、最短路问题的分类情况。 这告诉我们,写最短路问题时要考虑: 是否有权 是有向图还是无向图 是否有负环 有了思考的角度。 如果说上一篇文章是 让我们知道把大象装进冰箱要分成三步。 因为全部内容整合在一篇文章里有点长,所以把这篇文章分了俩部分 假设小镇中一个地方对应这张图的一个结点,你的出生点在古河面包店(0号位置),据题意,你需要一个地点都不落地走完整张图,这样才能收集完所有光玉。 先选择一条路一直往前走,走到尽头后,就返回到上一个交叉路口选择另一条没走过的路。 根据这个寻路的过程,我们要知道: 关于返回到上一个路口,我们很容易想到递归。 递归的过程是 走到每一个相邻的结点 递归函数: 到达(某点) 通过不断深入访问到 无法继续深入时,返回到上一个交叉路口。 整个DFS结束 我们都知道,递归是可以画出树的。 到这里DFS的介绍就结束啦 广度优先搜索(Breadth First Search)—— 听起来很迷糊,那下面看用BFS扫这个树就知道了。 很明显,先扫0点,然后扫1点和 7点,然后扫 4 和 5 然后扫 2、3、6 。 这里你知道了BFS遍历树的话,是一层一层地扫描, (这个问题曾经困扰了我很久,也是很多初学者的一个难点问题。恰恰因为这难点,使得很多人最开始上手的是DFS而不是BFS) 下面来讲讲如何去思考这个过程。 我们知道每个点的信息: 仔细琢磨扫描的步骤 听完这些,是不是隐约有点感觉了,但代码还是敲不出来。 再提示一下, 答: 可以写出伪代码: 代码看起来比DFS更简短, 通过了解刚刚的树上BFS,图上的BFS也能推理出。 至此,BFS遍历图结束。 DFS与BFS既是遍历图的方式,也是一种搜索的思想。 第一部分 DFS与BFS结束啦
可以让我们对求解最短路问题有个角度。
我们还需要掌握一些基本的工具。
那么 这篇文章就是 学习怎么打开冰箱门,怎么把大象放进去。正文开始
这里是Part 1 BFS与DFS
点这里去 Part 2 一些STL与如何存图
解最短路的必要基础(BFS与DFS,STL,如何存图)
DFS与BFS
问题引入

有一天,你穿越到Clannad(炒鸡好看的游戏与番剧)的小镇。你知道小镇上的每个地方与每条路。小镇的某些地方可能会藏有实现愿望的光玉。现在你要出发去收集小镇上所有的光玉。
如图:
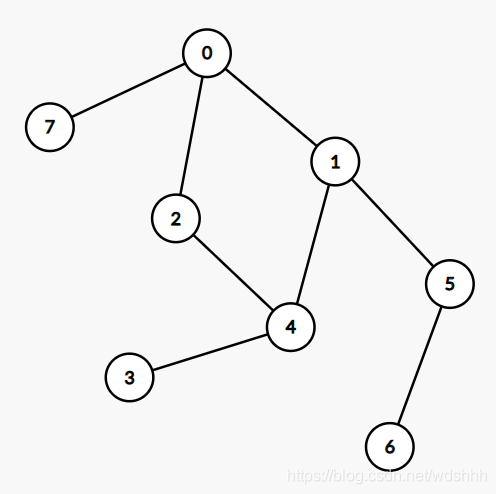
DFS
深度优先搜索(Depth First Search):
递归的边界是 走到尽头(即没有能走的结点 或者 每一个相邻结点都走完了)伪代码: 到达(P点){ for(从P点出发能去的相邻的点Q){ if(没有来过Q点){ 记录Q点到过了 到达(Q点) } } 返回P点前的一步 } 解析:
递归函数结束:当for循环(遍历所有能去的结点)结束过程:
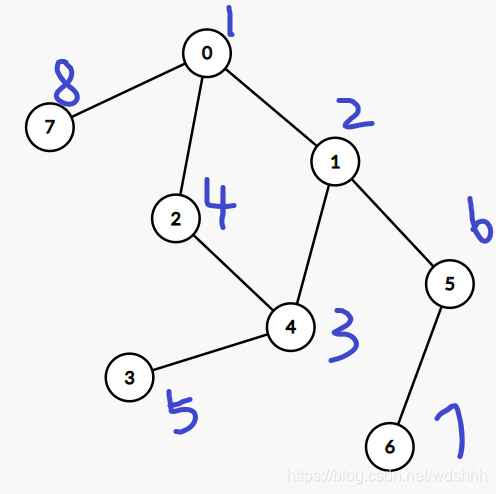
据说 下面的过程跟上面的图很配哦//从0点出发 , 记录0点到过了; 到了(0点) 开始遍历0点能去的相邻点(1点,2点,7点) 按照结点编号从小到大遍历的话(从大到小也可以完成DFS,只是顺序不一样,一般都是按照从小到大) //先到达1点 , 记录1点到达了 到了(1点) 开始遍历1点能去的相邻点(0点(被访问过,直接pass),4点,5点) //先到达4点, 记录4点到达了 到了(4点) 开始遍历4点能去的相邻点(1点(被访问过,直接pass),2点,3点) //先到达2点, 记录2点到达了 到了(2点) 开始遍历2点能去的相邻点(0点,1点) 0点和1点都被访问过了。 返回 //再到达3点, 记录3点到达了 到了(3点) (哪都不能走) 返回 //再到达5点, 记录5点到达了 到了(5点)(只能到达6点) //先到达6点, 记录6点到达了 到了(6点)(哪都不能走) 返回 这时2点被访问了,不能到达2点 //到达7点, 记录7点访问完了 到达(7点)(哪都不能走) 返回 返回 结束
所以这里给出此次遍历的DFS树:
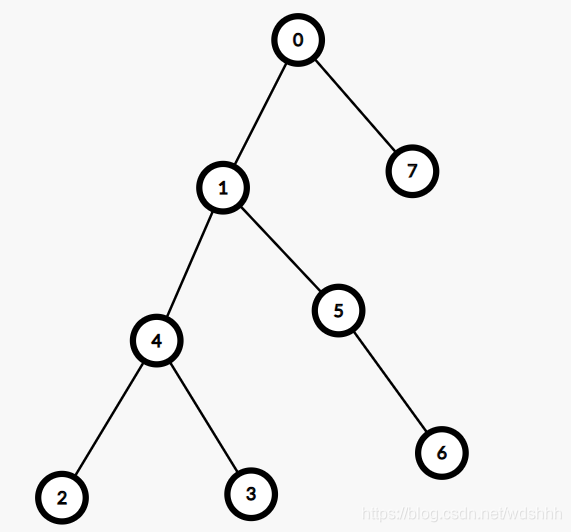
后序遍历这个树,就得到刚刚遍历整个图的过程。
如果有疑问,或者觉得文章有漏洞,何不在评论里指出来呢!(嘻嘻)BFS
从根开始(第一层),先扫完根的所有相邻点(第二层),再伸长手扫完第二层所有点的所有相邻点(第三层)…直到把最后一层都扫完。BFS引入
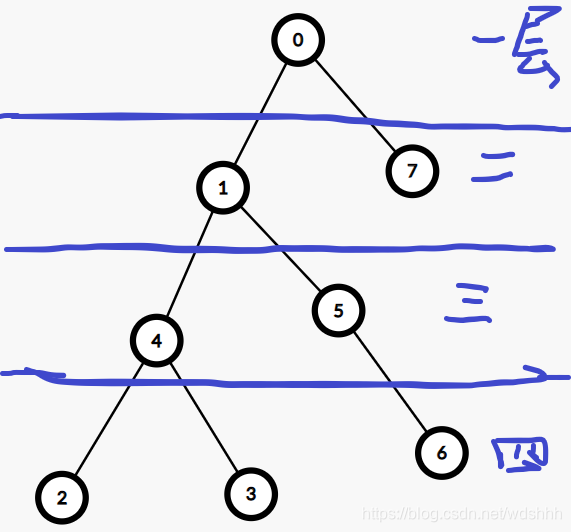
但可能会疑惑,我们只知道点跟哪些点相连,
在扫描了一个点后,怎么又突然跳到了离这个点的辣么远的点呢?(如扫完3点后,扫6点)
所以一开始搞不懂很正常,(给我自己的蒻找理由)BFS遍历树的过程讲解
1.编号
2.相邻点是哪些。
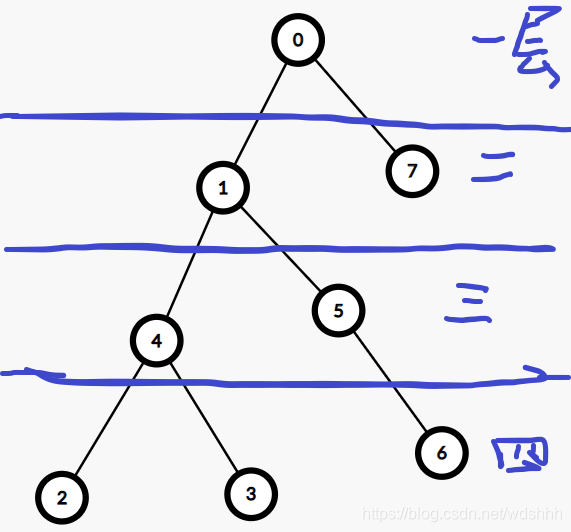
面对图论问题时,图片和过程更配哦第一层 扫描 0 点。 这时 由0点我们知道,下一层要扫描的是1点和7点。 那我们把1点和7点存在一个容器里,到下一层的时候拿出来。 第二层 扫描的是1 点和7点 。 恰好容器里仅有1点和7点。 分别把他们拿出来。 先把容器里的1点拿出来。由1点我们知道 下一层要扫描的是4点和5点。 那我们把4点和5点放进容器里,并且他们被拿出的次序是7点之后。(后进后出) 这时容器里有 7点 4点 5点。 第二层刚好还差7点没扫描完。(先进先出) 再把7点拿出来。由7点我们知道 下一层要扫描的是 空 … 第三层 扫描的是4点和5点。 恰好容器里仅有4点和5点 继续重复第二层一样的动作。 4点拿出,知道第四层要扫描2点 3点,把2点3点放入容器。 5点拿出,知道第四层要扫描6点,把6点放入容器。 第四层 扫描的是2点3点6点 拿出2点,放入空(啥都不放入)。 拿出3点,放入空。 拿出6点,放入空。 这时,第四层扫描完了,那么!怎么判断是否有第五层呢? 图中明显没有第五层。 而容器也没有东西了。 由前面我们知道,容器每次都能在扫描完当前层后,保留下一层要扫描的点。 那么!!! 当容器中没有东西的时候就代表:所有层数已经扫完了,OVER。
容器是什么,每层的操作是重复的吗?这种重复操作是怎么停止的?
容器具有先进先出,后进后出的特点。当然是——队列。
每次的操作是重复的,那就是要用上循环。
循环结束的条件就是:队列为空时。放入0点到队列里。 while(队列不为空){ 取出队列里的一个点为A。 弹出A for(遍历A点所有相连的点) (把所有相连的点放入队列) } 但理解着实更困难些 。对于图上的BFS
放入0点到队列里。 while(队列不为空){ 取出队列里的一个点为A。 弹出A for(遍历A点所有相连的点){ if(该点没有被访问过) { 记录该点访问过 该点入队列 } } } 
小结
一个是比较笨的办法 不断尝试,走到底再走其他路。
一个是一层一层的把所有结点走完。
点这里 进入第二部分 一些STL与存图的三种方法
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)