1. 原理
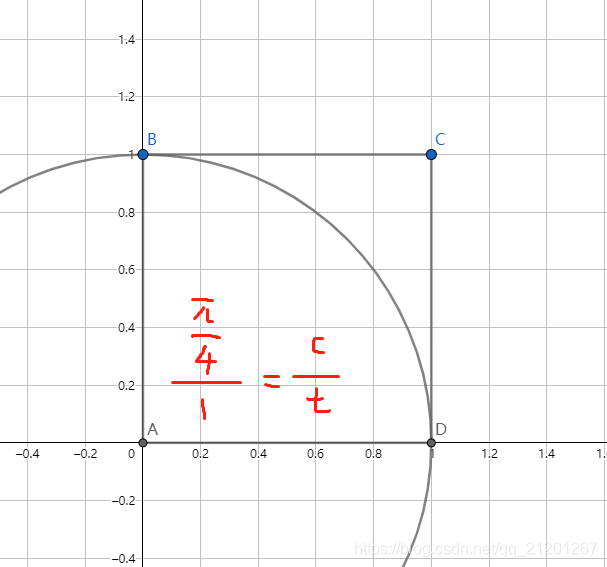
x∈[0,1),y∈[0,1) 的均匀分布随机点,模拟
t 次,落在以
(0,0) 为圆心,半径
r=1 的圆以内的次数为
c
4π≈tc⇒π≈4c/t2. 模拟代码
# -*- coding:utf-8 -*- # @Python Version: 3.7 # @Time: 2020/5/2 9:02 # @Author: Michael Ming # @Website: https://michael.blog.csdn.net/ # @File: monte_carlo_cal_pi.py # @Reference: import random import matplotlib.pyplot as plt simulations = [100, 1000, 10000] plt.figure() plt.rcParams['font.sans-serif'] = 'SimHei' # 消除中文乱码 plotid = 1 color = ['r', 'b'] for i in range(len(simulations)): f = plt.subplot(1, 3, plotid) plotid += 1 count = 0 t = simulations[i] time = simulations[i] while time > 0: time -= 1 x = random.random() # [0,1) y = random.random() # [0,1) val = x ** 2 + y ** 2 pos = 1 if (val < 1): pos = 0 count += 1 f.scatter(x, y, c=color[pos]) pi = 4 * count / t f.set_title("模拟次数{},pi的值{:.4f}".format(t, pi)) plt.suptitle("蒙特卡罗法近似求解圆周率pi") plt.show() 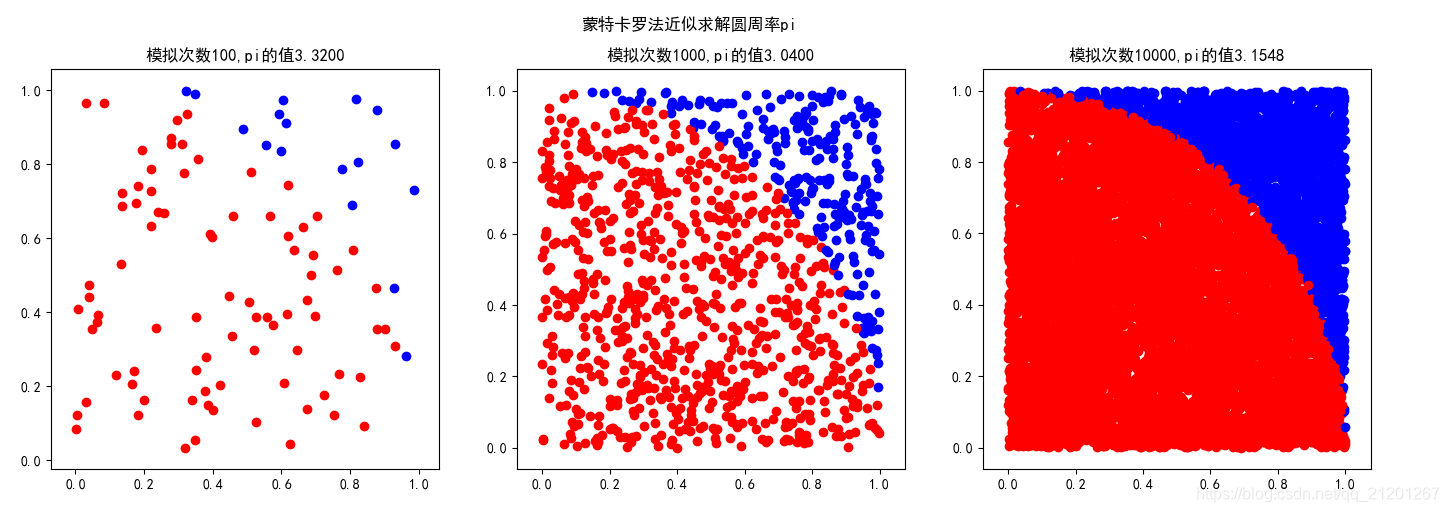
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)