面试官:小伙子，你给我简单介绍下排序算法吧数据结构与算法清风~的博客-

1、冒泡排序

最简单的一种排序算法。假设长度为n的数组arr，要按照从小到大排序。则冒泡排序的具体过程可以描述为：首先从数组的第一个元素开始到数组最后一个元素为止，对数组中相邻的两个元素进行比较，如果位于数组左端的元素大于数组右端的元素，则交换这两个元素在数组中的位置，此时数组最右端的元素即为该数组中所有元素的最大值。接着对该数组剩下的n-1个元素进行冒泡排序，直到整个数组有序排列。
算法的时间复杂度为O(n^2)

// 冒泡排序 void BubbleSort(int arr[], int length) { for (int i = 0; i < length; i++) { for (int j = 0; j < length -  i - 1; j++) { if (arr[j] > arr[j + 1]) { int temp;     temp = arr[j + 1];     arr[j + 1] = arr[j];     arr[j] = temp; } } } } 

2、插入排序

插入排序的基本思想就是将无序序列插入到有序序列中。
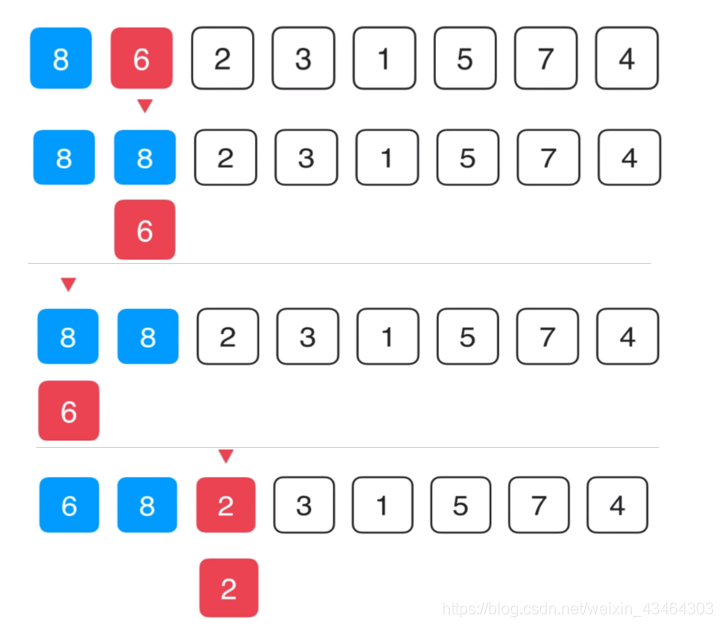
例如要将数组arr=[8,6,2,3,1,5,7,4]排序，第0个索引8的位置不变，第一个元素6复制一份，保存起来，来看6这个元素是不是应该放在当前这个位置。方法就是，看6这个位置与当前位置前一个位置8进行比较，6比8小，8往后挪下，之后再来考察6是不是应该放在前一个位置。此时，6已经是第0个位置了，就不需要再改变了。
下面到2这个元素，2拿出来，2比8小，把2的位置的值赋值为8，2放到前一个位置去，以此往复
时间复杂度是O(n^2)

 public static void InsertionSort(Comparable[] arr){ int n = arr.length; for (int i = 0; i < n; i++) { // 寻找元素arr[i]合适的插入位置 //arr[i]存放再一个新的元素中         Comparable e = arr[i]; //j保存元素e应该插入的位置 //arr[j-1].compareTo(e) > 0 这个位置的元素是不是比e还要大 //说明当前找到的j还不是元素e最终的位置，所以循环要继续 int j = i; for(; j > 0 && arr[j-1].compareTo(e) > 0 ; j--)             arr[j] = arr[j-1];         arr[j] = e; } } } 

3、归并排序o

“归并”的含义是将两个或两个以上的有序序列组合成一个新的有序表。先左边的数组先排序，右边的数组排序，再归并起来。
时间复杂度是O(nlogn)

当前已经排好序的元素，1和2两个元素谁先放到第一个位置，1比2小，先放1 。

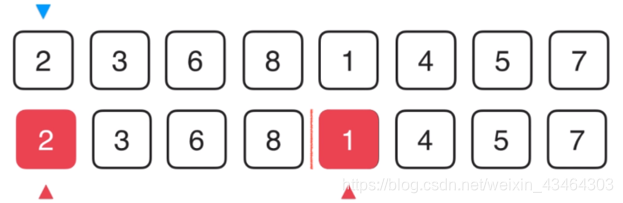
那么蓝色的箭头就可以考虑下一个位置，1这个位置就可以到下一个位置了，考虑2和4谁更小。

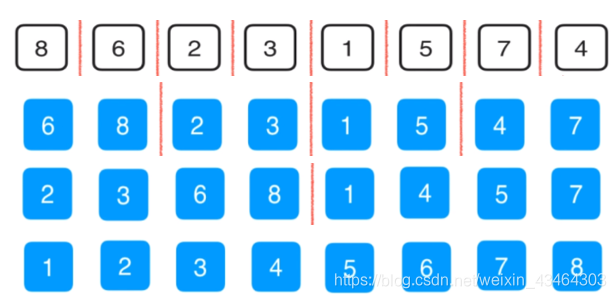
public class MergeSort{ // 将arr[l...mid]和arr[mid+1...r]两部分进行归并 private static void merge(Comparable[] arr, int l, int mid, int r) { //需要一个临时的辅助空间，空间大小就是当前处理的空间一样大         Comparable[] aux = Arrays.copyOfRange(arr, l, r+1); // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1 int i = l, j = mid+1; for( int k = l ; k <= r; k ++ ){ //先判断索引的合法性 if( i > mid ){ // 如果左半部分元素已经全部处理完毕                 arr[k] = aux[j-l]; j ++; } else if( j > r ){ // 如果右半部分元素已经全部处理完毕                 arr[k] = aux[i-l]; i ++; } else if( aux[i-l].compareTo(aux[j-l]) < 0 ){ // 左半部分所指元素 < 右半部分所指元素                 arr[k] = aux[i-l]; i ++; } else{ // 左半部分所指元素 >= 右半部分所指元素                 arr[k] = aux[j-l]; j ++; } } } // 递归使用归并排序,对arr[l...r]的范围进行排序 private static void sort(Comparable[] arr, int l, int r) { //递归到底的情况，l大于等于r，就是代表只有一个元素 ，甚至一个元素都没有 //代表数据集为空 if (l >= r) return; int mid = (l+r)/2; sort(arr, l, mid); sort(arr, mid + 1, r); //然后排序好了，就是实现mrege merge(arr, l, mid, r); } public static void sort(Comparable[] arr){ int n = arr.length; sort(arr, 0, n-1); } } 

4、快速排序

快速排序的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，已达到整个序列有序。o
把4这个元素挪到它再排好序的时候应该所处的位置，4这个元素有一个性质，就是4之前的元素都是小于4的，4之后的都是大于4
时间复杂度是O(nlogn)


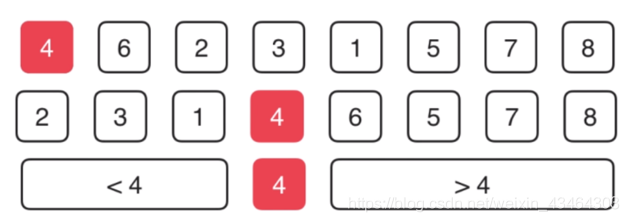
如果当前的这个元素e比v还要大，放在大于v的后面 ，去讨论下一个元素i++
但是如果e小于v，那么就要想办法把e放到橙色部分，把橙色 j 后面所指的最后一个元素和当前考察的 i 的元素，进行位置交换，那么 j++

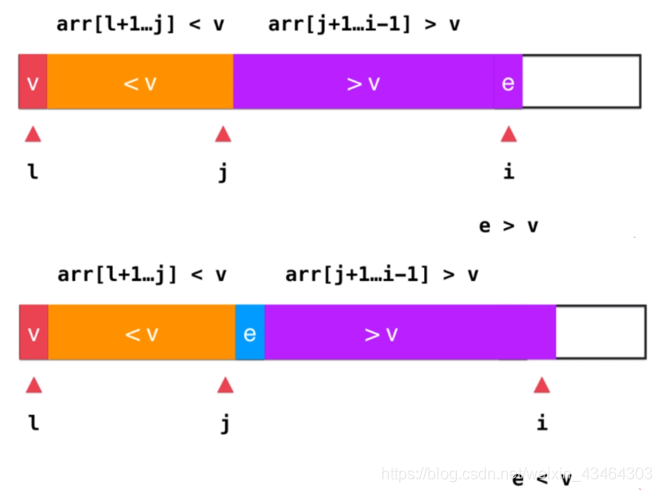
public class QuickSort { // 对arr[l...r]部分进行partition操作 // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p] private static int partition(Comparable[] arr, int l, int r){ //取这个数组中第一个元素         Comparable v = arr[l]; //从l+1开始逐步遍历整个数组 //i是取不到的，所以需要后开 //初始化时l，就时比l+1还要小，arr[l+1...j]这个区间为空的 int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v for( int i = l + 1 ; i <= r ; i ++ ) //arr[i]大于v就是i++ ，什么都不需要做，因为循环已经给了 //关键是arr[i]小于v的时候，才需要j++ if( arr[i].compareTo(v) < 0 ){                 j ++; //进行交互操作 swap(arr, j, i); } //最后就是将l与j位置进行交互 swap(arr, l, j); return j; } // 递归使用快速排序,对arr[l...r]的范围进行排序 private static void sort(Comparable[] arr, int l, int r){ //递归到底的函数进行处理 if( l >= r ) return; //下面使用快速排序的过程 int p = partition(arr, l, r); sort(arr, l, p-1 ); sort(arr, p+1, r); } public static void sort(Comparable[] arr){ int n = arr.length; sort(arr, 0, n-1); } private static void swap(Object[] arr, int i, int j) {         Object t = arr[i];         arr[i] = arr[j];         arr[j] = t; } } 

5、堆排序

堆看做是一个完全二叉树。每个结点的值总是不大于其父节点的值，堆总是一个完全二叉树。
时间复杂度是O(nlogn)

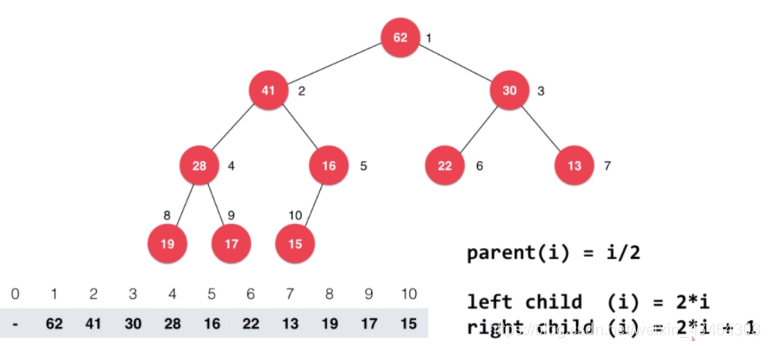
将待排序列构造成一个大顶堆(或小顶堆)，整个序列的最大值(或最小值)就是堆顶的根结点，将根节点的值和堆数组的末尾元素交换，此时末尾元素就是最大值(或最小值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值(或次小值)，如此反复执行，最终得到一个有序序列。

5为根的堆不满足堆的性质，在这个位置上面执行shift，
4 为根节点不满足堆性质，8 比5还要大，4与8交换位置。以此往复

public class HeapSort { public static void sort(Comparable[] arr){ int n = arr.length; // 注意，此时我们的堆是从0开始索引的 // 从(最后一个元素的索引-1)/2开始 // 最后一个元素的索引 = n-1 for( int i = (n-1-1)/2 ; i >= 0 ; i -- ) shift(arr, n, i); //i是倒数第一个元素开始 for( int i = n-1; i > 0 ; i-- ){ //把当前最大的元素和arr[i]位置的元素交换 swap( arr, 0, i); shift(arr, i, 0); } } // 交换堆中索引为i和j的两个元素 private static void swap(Object[] arr, int i, int j){         Object t = arr[i];         arr[i] = arr[j];         arr[j] = t; } // 翻转shift过程 private static void shift(Comparable[] arr, int n, int k){ while( 2*k+1 < n ){ int j = 2*k+1; //判断有可能也没有右孩子 //右孩子也比左孩子还大，就交换一下 if( j+1 < n && arr[j+1].compareTo(arr[j]) > 0 )                 j += 1; //如果这个父亲节点还是大于它的两个孩子节点，就不需要转换 if( arr[k].compareTo(arr[j]) >= 0 ) break; swap( arr, k, j);             k = j; } } }