其他不再具体说明。 下面对各种类型的自适应滤波算法进行简单的总结分析。 已把音频放在了 https://pan.baidu.com/s/1L5vXa60c0wEATx2LQVLp-Q
我要讲的几种方法
绪论
自适应滤波的基本原理

自适应滤波算法
自适应滤波算法种类
最小均方误差算法(LMS)
e(n)=d(n)−XT(n)W(n)W(n+1)=W(n)+2ue(n)X(n)其中 u 是步长因子,LMS算法的收敛条件是
0<u<1/λmax,
λmax是输入信号自相关矩阵的最大特征值。
u(n)=β(1+e−α∣e(n)∣1)该算法能同时获得较快的收敛速度、跟踪速度和较小的稳态误差。然而,该Sigmoid函数过于复杂,且在误差e(n)接近零处变化太大。不具有缓慢变化的特性,使得SVSLMS算法在自适应稳态阶段仍有较大的步长变化,这是该算法的不足。递推最小二乘算法(RLS)
J(n)=i=0∑nλn−i⋅∣e(i)∣2最小。
Rxx(n)的逆进行递推估计更新,收敛速度快,其收敛性能与输入信号的频谱特性无关。
Rxx(n)=E[λn−iXXT]可以得出RLS算法的基本关系:
W(n)=W(n−1)+k(n)e(n−1)
其中
k(n)=λ+XT(n)P(n−1)X(n)P(n−1)X(n),P(n−1)=Rxx−1(n)
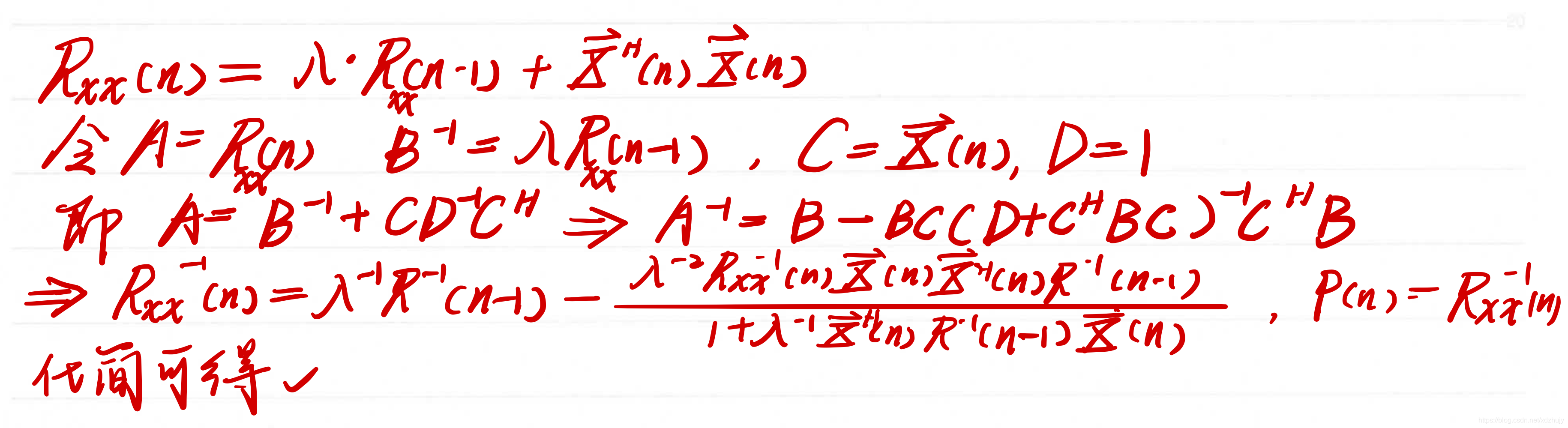
Rxx(n)的逆失去了正定特性,这还将引起算法发散。为了降低RLS算法的计算复杂度,并保留RLS算法收敛速度快的特点,产生了许多改进的RLS算法。如快速RLS(Fast RLS)算法,快速递推最小二乘格型(Fast Recursive Least Squares Lattice)算法等。这些算法的计算复杂度低于RLS算法,但它们都存在数值稳定性问题。变换域自适应滤波算法
X′=T∗X
W(n+1)=W(n)+2ue(n)P−1(n)X(n)
P(n)=diag[P(n,0),P(n,1),…,P(n,N−1)]
P(n,l)=βP(n−1,l)+(1−β)XT(n,l)⋅X(n,l),l=0,1…N−1若令
Λ2=P(n),则权系数向量的迭代方程为:
W(n+1)=W(n)+2ue(n)Λ−2X(n)仿射投影算法
Y(k)=XT(k)[W(k−1)+ΔW(k−1)]其中:
Y(k)=[y(k),y(k−1),…,y(k−p+1)]
X(k)=[x(k),x(k−1),…,x(k−p+1)]
利用矩阵的广义逆可求得
ΔW(k−1),因此,仿射投影算法可表示为:
e(k)=Y(k)−XT(k)W(k−1)
g(k)=[XT(k)X(k)+δl]−1e(k)
W(k)=W(k−1)+uΔW(k−1)=W(k−1)+uX(k)g(k)其他
自适应滤波算法性能评价
自适应滤波的Matlab仿真
正弦信号加噪的LMS自适应滤波
代码
clc,clear,close all; g=100; L=1024;%信号长度 k=128;%滤波器阶数 pp=zeros(g,L-k); u=0.001; for q=1:g t=1:L; a=1; s=a*sin(0.05*pi*t); figure(1); subplot(311); plot(s); title('信号s时域波形'); xlabel('n'); axis([0,L,-a-1,a+1]); xn=awgn(s,5); %信噪比5dB的WGN y=zeros(1,L); y(1:k)=xn(1:k); w=zeros(1,k); e=zeros(1,L); for i=(k+1):L XN=xn((i-k+1):(i)); y(i)=w*XN'; e(i)=s(i)-y(i); pp(i)=pp(i)+e(i); w=w+u*e(i)*XN; end end subplot(312) plot(xn); title('信号加高斯白噪声后的时域波形'); axis([0,L,-a-2,a+2]); subplot(313) plot(y); axis([0,L,-a-1,a+1]); title('LMS算法自适应滤波后的输出时域波形'); 结果
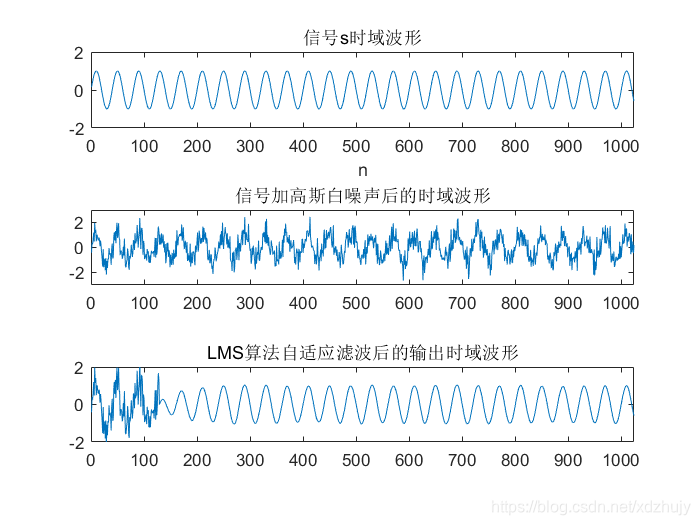
音频信号Rolling in the Deep的LMS自适应滤波
音频资源
提取码:vs7o代码
function [y,W,e]=LMSfilter(xn,d,L,mu) % 输入参数: % xn 输入的信号序列 (列向量) % d 所期望的响应序列 (列向量) % L 滤波器的阶数 (标量) % mu 收敛因子(步长) (标量) 要求0<mu<xn的相关矩阵最大特征值的倒数 % 输出参数: % W 滤波器的权值矩阵 (矩阵) % 大小为M x t, % e 误差序列(t x 1) (列向量) % y 实际输出序列 (列向量) t = length(xn); e = zeros(t,1); % 误差序列,en(k)表示第k次迭代时预期输出与实际输入的误差 W = zeros(L,t); % 每一行代表一个加权参量,每一列代表-次迭代,初始为0 % 迭代计算 for k = L:t % 第k次迭代 x = xn(k:-1:k-L+1); % 滤波器L个抽头的输入 y = W(:,k-1).'*x; % 滤波器的输出 e(k) = d(k)- y ; % 第k次迭代的误差 W(:,k) = W(:,k-1) + 2*mu*e(k)*x; % 滤波器权值计算的迭代式 end % 求最优时滤波器的输出序列 r如果没有yn返回参数可以不要下面的 y = inf * ones(size(xn)); % inf 是无穷大的意思 for k = L:length(xn) x = xn(k:-1:k-L+1); y(k) = W(:,end).'* x;%用最后得到的最佳估计得到输出 end
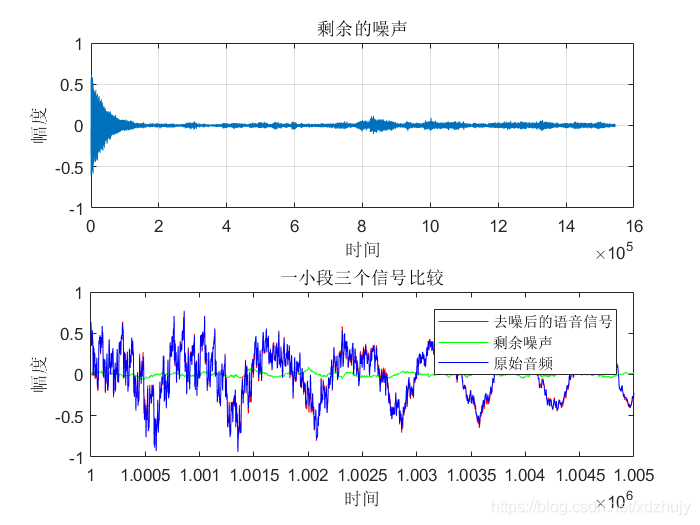
clc; clear all; close all; %% 产生信号源 [X,Fs] = audioread('Rolling in the Deep.wav');%音频过长无法计算自相关 signal = X(:,1); %取出双通道中其中一个通道作为信号源signal audiowrite('原始音频.wav',signal,Fs); %创建原始音频.wav n = length(signal); t=(0:n-1); figure(1); subplot(3,1,1); plot(t,signal);grid;ylim([-2 2]); ylabel('幅度'); xlabel('时间'); title('原始音频信号'); %% 产生期望信号 dn = awgn(signal,10); %加入信噪比为10dB的高斯白噪声 noise=dn-signal; audiowrite('含噪音频.wav',dn,Fs); %创建含噪音频 subplot(3,1,2); plot(t,dn);grid;ylim([-2 2]); ylabel('幅度'); xlabel('时间'); title('含噪音频信号'); %% LMS滤波算法 M = 128; %滤波器阶数M u = 0.0004; %滤波器的步长 [yLMS,W,eLMS] =LMSfilter(noise,dn,M,u); %% 绘制去噪后的语音信号 subplot(3,1,3); plot(t,eLMS);grid;ylim([-2 2]); ylabel('幅度'); xlabel('时间'); title('去噪后的音频信号'); audiowrite('去噪音频.wav',eLMS,Fs);%保存去除噪声的音频 %% e = signal-eLMS;%剩余噪声 figure(2); subplot(2,1,1); plot(t,e);grid; ylabel('幅度'); xlabel('时间'); title('剩余的噪声'); %% 一小段三个信号比较 subplot(2,1,2); t=(1000000:1005000); plot(t,eLMS(1000000:1005000,1 ),'r',t,e(1000000:1005000,1),'g',t,signal(1000000:1005000,1),'b'); axis([1000000,1005000,-1,1]); ylabel('幅度'); xlabel('时间'); legend('去噪后的语音信号','剩余噪声','原始音频'); title('一小段三个信号比较'); 结果及分析

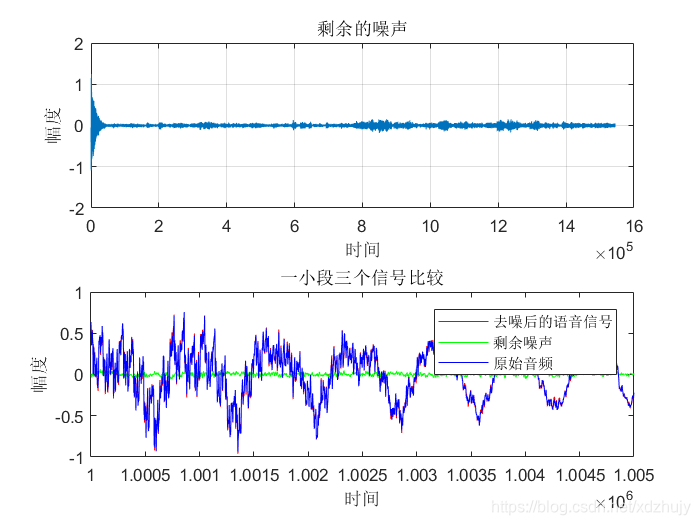
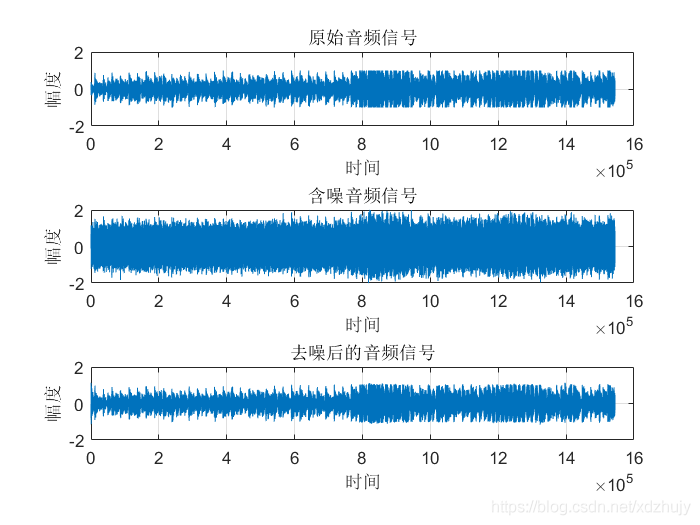
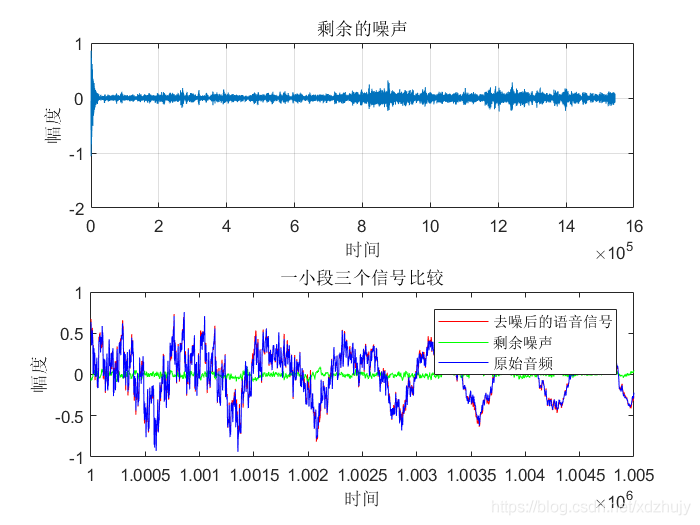
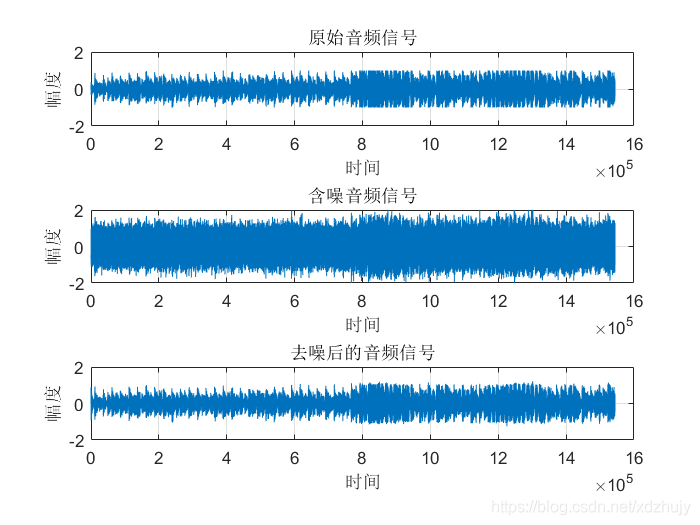
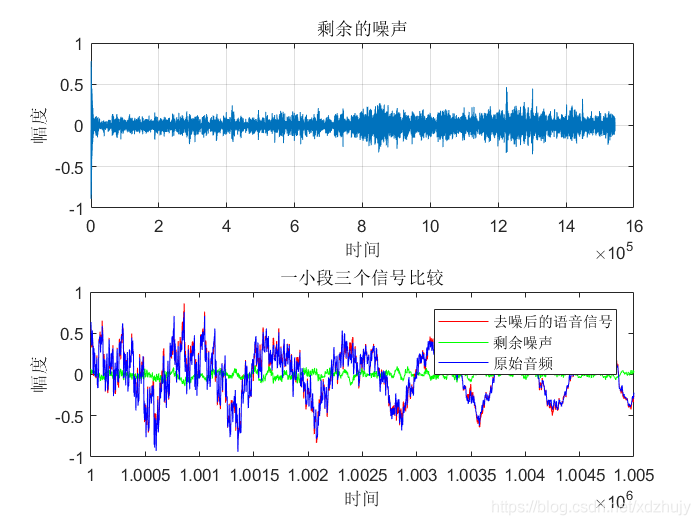
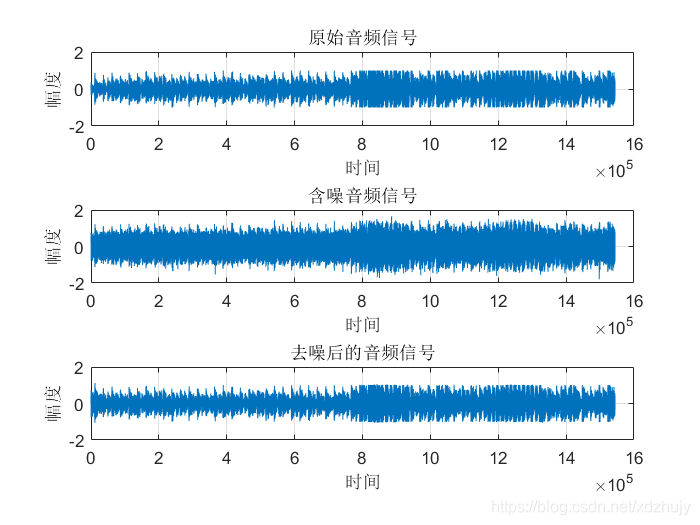
其他
J=wiener2(I,[M,N],noise); %表示M*N大小邻域局部图像均值与偏差,采用像素自适应滤波器对图像I滤波 参考文献
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)