后面几题都自己暴力对拍了一下,可能还会有错大家可以参考。 我们可以直接手算,或者求稳的话随便枚举一下所有情况就好了,下面是用的状态枚举。 参考代码: 用全排列函数直接算一下字符串的全排列就好了,可以用set维护一下防止有重复情况。 答案; 2520 参考代码: 基本思路: 很简单,我们先写个26个字母的表,每次算一下原字符字母对应位置往前3个就行了注意是循环数组,模一下26就好了。 参考代码: 签到题,随便搞。 参考代码: 比较麻烦的模拟,先把这个螺旋数组打出来再找就是了,具体模拟过程可以参考代码。 参考代码: 基本思路: 这题我们看一下就会发现很像一个dp,但是如果朴素的去dp的话,设 参考代码: 基本思路: 这题看上去复杂其实比较简单,每个村庄之间两两连边然后跑一个MST就行了,这里是用的Kurskal算法,并查集实现。 ps.这题注意一下那个公式里h的位置在外面。 参考代码: 基本思路: ps.越想越假,别学。 参考代码:
蓝桥杯省模拟赛
第一题:
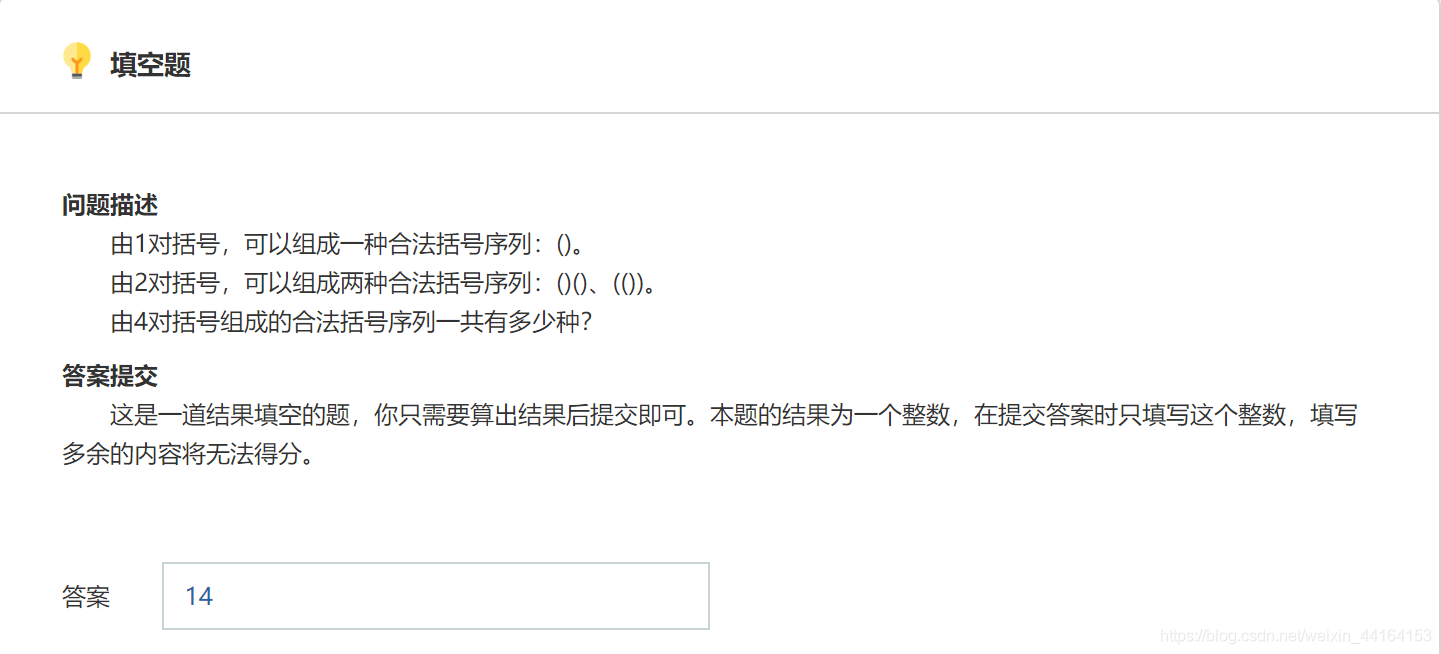
基本思路:
答案: 14#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define ll long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } bool can(string s){ int cnt = 0,n = s.size(); for(int i = 0 ; i < n ; i++){ if(s[i] == '(') cnt++; else{ cnt--; if(cnt < 0) return false; } } return cnt == 0; } signed main() { IO; int ans = 0; for(int i = 0 ; i < (1 << 8) ; i++){ string str; int cnt = 0; for(int j = 0 ; j < 8 ; j ++){ if(i >> j & 1){ str += '('; cnt++; }else { str += ')'; } } if(cnt != 4) continue; if(can(str)) ans++; } cout << ans << 'n'; return 0; } 第二题:

这个没啥好说的边最少的无向连通图就是树,n-1条边
答案: 2018第三题:

基本思路:#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define ll long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } signed main() { IO; string str = "LANQIAO"; sort(str.begin(),str.end()); set<string> st; do{ st.insert(str); }while (next_permutation(str.begin(),str.end())); cout << st.size() << 'n'; return 0; } 第四题:
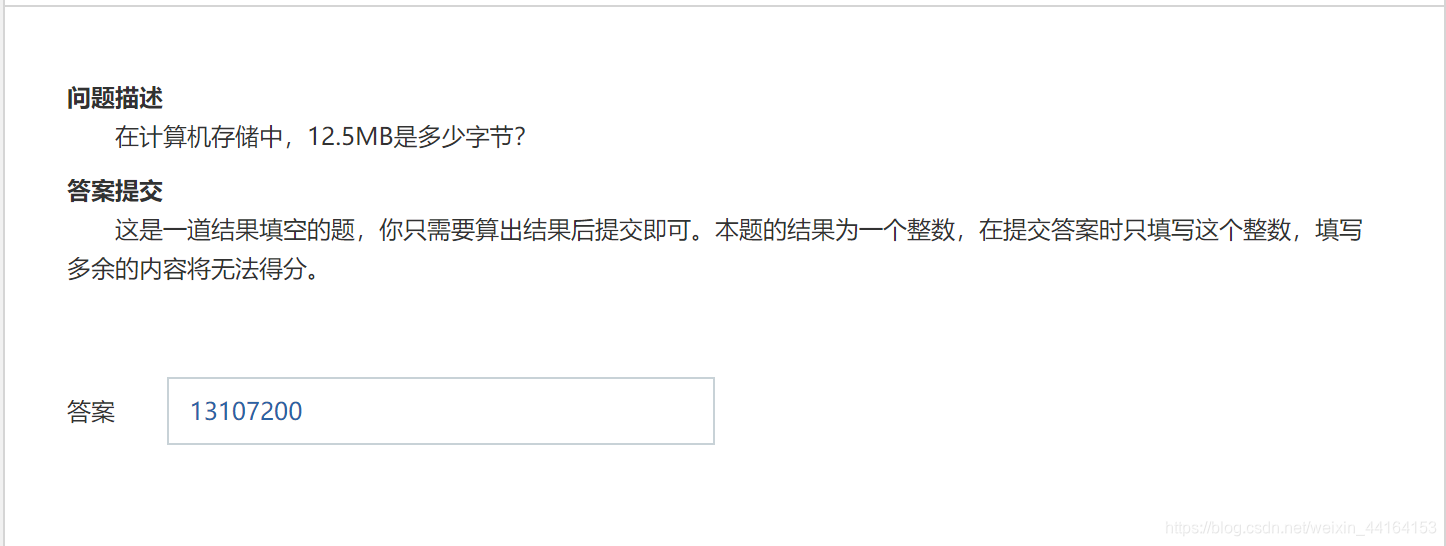
这也没啥好说的,直接手算,或者写个代码打印一下答案就好了。
答案: 13107200第五题:


#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define ll long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } string ck = "abcdefghijklmnopqrstuvwxyz"; string str; signed main() { IO; cin >> str; string ans; for(int i = 0 ; i < (int)str.size() ; i++){ int t = str[i] - 'a'; int nt = (t + 3) % 26; ans += ck[nt]; } cout << ans << 'n'; return 0; } 第六题:


基本思路:#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define ll long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } int n,a,b,c; int ans = 0; signed main() { IO; cin >> n; cin >> a >> b >> c; rep(i,1,n){ if(i % a != 0 && i % b != 0 && i % c != 0) ans++; } cout << ans << 'n'; return 0; } 第七题:


基本思路:#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define ll long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } const int maxn = 1020; int n,m; int res[maxn][maxn]; void solve(){ int l = 1,t = 1,r = m,k = n; int cnt = 0; while(true){ for(int i=l;i<=r;i++){ res[t][i]=++cnt; if(cnt >= n * m) return; } t++; for(int i=t;i<=k;i++){ res[i][r]=++cnt; if(cnt >= n * m) return; } r--; for(int i=r;i>=l;i--){ res[k][i]=++cnt; if(cnt >= n * m) return; } k--; for(int i=k;i>=t;i--){ res[i][l]=++cnt; if(cnt >= n * m) return; } l++; } } signed main() { IO; cin >> n >> m; solve(); int r,c; cin >> r >> c; cout << res[r][c] << 'n'; return 0; } 第八题:


dp[i][j]表示在第i个位置,这个位置的数字是j,我们可以得到这样的转移方程即:dp[i][j] = dp[i-1][k](i 是奇数时 j > k , i 是偶数时 j < k) 这样我们需要枚举i,j,k复杂度为O(n^3)肯定过不了100%数据。这时候我们发现k这个部分只有大小关系,所以可以直接用之前答案的前缀和来优化一下,那么优化后复杂度为O(n^2)就能过了。
ps.其实直接开一维dp数组重复使用就是了,不愿改了。#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define int long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } const int maxn = 1050; const int mod = 10000; int m,n; int dp[maxn][maxn]; int sum[maxn]; signed main() { IO; cin >> m >> n; for(int i = 1; i <= n; i++){ dp[1][i] = 1; } for(int i = 1 ; i <= n; i++){ sum[i] = (sum[i-1] + dp[1][i]) % mod; } for(int i = 2 ;i <= m; i++){ for(int j = 1 ; j <= n; j++){ if(i & 1){ dp[i][j] = (dp[i][j] + sum[j-1]) % mod; }else{ dp[i][j] = (dp[i][j] + sum[n] - sum[j] + mod) % mod; } } sum[0] = 0; for(int j = 1 ; j <= n; j++){ sum[j] = (sum[j-1] + dp[i][j]) % mod; } } int ans = 0; for(int i = 1; i <= n; i++){ ans += dp[m][i]; ans %= mod; } cout << ans << 'n'; return 0; } 第九题:



#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define int long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } const int maxn = 1010; int n; int par[maxn]; void init(){ rep(i,0,n) par[i] = i; } int find(int x){ return par[x] == x ? x : par[x] = find(par[x]); } void unite(int x,int y){ x = find(x),y = find(y); if(x != y) par[x] = y; } bool same(int x,int y){ return find(x) == find(y); } struct Edge{ int u,v; double w; Edge(int _u,int _v,double _w){ u = _u,v = _v,w = _w; } bool operator < (const Edge &e) const{ return w < e.w; } }; struct Point{ int x,y,h; }p[maxn]; double dis(Point a,Point b){ return sqrt((double)(a.x - b.x) * (a.x - b.x) + (double)(a.y - b.y) * (a.y - b.y)) + (double)(a.h - b.h) * (a.h - b.h); } signed main() { cin >> n; init(); rep(i,1,n){ cin >> p[i].x >> p[i].y >> p[i].h; } vector<Edge> vec; rep(i,1,n){ rep(j,1,i-1){ double w = dis(p[i],p[j]); vec.push_back(Edge(i,j,w)); } } sort(vec.begin(), vec.end()); // for(auto it : vec){ // cout << it.u << " " << it.v << " " << it.w << 'n'; // } double ans = 0; for(int i = 0 ; i < (int)vec.size() ;i++){ int u = vec[i].u,v = vec[i].v; if(!same(u,v)){ unite(u,v); ans += vec[i].w; } } printf("%.2lfn",ans); return 0; } 第十题:



计算几何+贪心,稍微有些麻烦,我们发现这个n比较小,我们直接贪心一下每次优先取r大的,即先对每个人按照树的半径排个序,然后每次将新树加进来的时候,和已经在答案里的每棵树都比一下看是不是是会相交(这里直接比两圆心距离和两个圆的半径就可以了),不会相交就加入答案,相交就尝试下一个, 基本确定是个假做法,真做法因为范围比较小可能可以暴力dp一下?n <= 20的话枚举状态应该可以搞,但是可能比较麻烦,这里就不写了。#pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits/stdc++.h> using namespace std; #define IO std::ios::sync_with_stdio(false) #define ll long long #define rep(i, l, r) for (int i = l; i <= r; i++) #define per(i, l, r) for (int i = l; i >= r; i--) #define mset(s, _) memset(s, _, sizeof(s)) #define pb push_back #define pii pair <int, int> #define mp(a, b) make_pair(a, b) #define INF 0x3f3f3f3f inline int read() { int x = 0, neg = 1; char op = getchar(); while (!isdigit(op)) { if (op == '-') neg = -1; op = getchar(); } while (isdigit(op)) { x = 10 * x + op - '0'; op = getchar(); } return neg * x; } inline void print(int x) { if (x < 0) { putchar('-'); x = -x; } if (x >= 10) print(x / 10); putchar(x % 10 + '0'); } const int maxn = 1010; struct Point{ int a,b,c; bool operator < (const Point &p) const{ return c > p.c; } }s[maxn],s2[maxn]; int n,res = 0; signed main() { IO; cin >> n; rep(i,0,n-1) cin >> s[i].a >> s[i].b >> s[i].c; sort(s,s+n); int p = 0; for(int i = 0 ; i < n; i++){ int ok = 1; for(int j = 0 ;j < p ; j++){ double d = sqrt((s[i].a-s2[j].a)*(s[i].a-s2[j].a)+(s[i].b-s2[j].b)*(s[i].b-s2[j].b)); if(d < (double)(s[i].c + s2[j].c)){ ok = 0; break; } } if(ok){ s2[p++] = s[i]; res += s[i].c * s[i].c; } } cout << res << 'n'; return 0; }

本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)