坐标形式: 复数集E内的每一个复数z=a+b*i,都有(唯一确定的/无穷多个/有限个)复数 零点:分子为零的点,即G(s)=0时,s=z1,z2叫做G(s)的零点; 极点:分母为零的点,即G(s)=∞时,s=p1,p2叫做G(s)的极点; 拉氏变换是将时间函数f(t)变换为复变函数F(s)的函数。拉氏变换建立了时域与复频域(s域)之间的联系。 式中,s=a+b*i为复变数,f(t)又称为原函数,F(s)又称为象函数。 拉氏变换是将时间函数F(s)变换为复变函数f(t)的函数。 式中,s=a+b*i为复变数,f(t)又称为原函数,F(s)又称为象函数。 欧拉公式:e^iθ=cosθ+isinθ, 推倒可得:(正余弦函数拉氏变换推导使用) sinθ=(e^iθ-e^-iθ)/2i cosθ=(e^iθ+e^-iθ)/2i 单位阶跃函数: 单位脉冲函数: 单位斜坡函数: 指数函数: 正弦函数: 余弦函数: 幂函数: 齐次性:L[a*f(t)]=a*F(s)、叠加性: 线性性质: L[df(t)/dt]=s*F(s)-f(0) 同理可得f(t)的各阶导数的拉氏变换时: L[d^2f(t)/dt]=s^2*F(s)-s*f(0)-f'(0) L[d^3f(t)/dt]=s^3*F(s)-s^2*f(0)-s*f'(0)-s”(0)……. L[t*f(t)]=-dF(s)/d(s)、 L[t^2*f(t)]=-d^2F(s)/d(s^2)、 ……、 L[t^n*f(t)]=-d^nF(s)/d(s^n) 多重积分: L[e^(-at)*f(t)]=F(s+a) L[f(t-a)]=e^(-a)*F(s),函数f(t-a)为函数f(t)延时间轴延迟了a。 原函数在t=0处的初值,等于s*【F(s)的终值】 原函数在t=+∞处的终值,等于s*【F(s)的初值】 两个原函数卷积的拉氏变换=它们象函数的乘积 L[f(t)*g(t)]=F(s)*G(s) 拉氏逆变换有三种方法:查表法、留数定理法、部分分式法。 1、查表法:由拉氏变换表直接查出与像函数F(s)对应的原函数f(t)。 2、留数定理法:利用留数定理计算像函数的原函数。 3、部分分式法:先把像函数分解为部分分式,再对各个分式进行逆变换。 这里给出了拉氏逆变换例题的网址,读者可以自行练习。 https://wenku.baidu.com/view/d6335d6f3968011ca300915a.html
一、复数和复变函数
1、复数的三种表现形式:
三角形式:
指数形式:
2、复变函数:
与之对应,可以确定(单值/多值)复变函数。
3、零点和极点
二、拉氏变换
1、拉氏变换
2、拉式逆变换
3、典型时间函数的拉氏变换
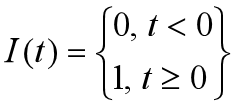 ,
, 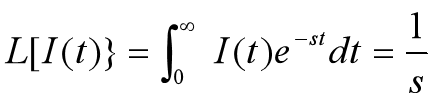

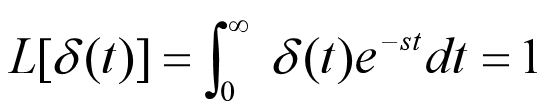
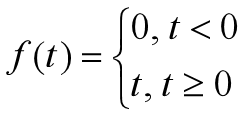


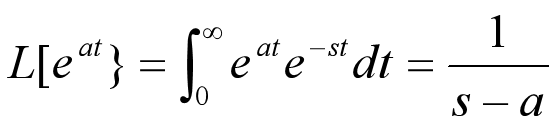
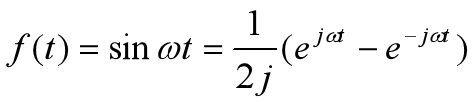

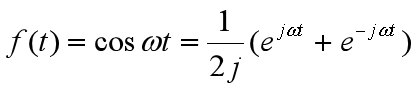
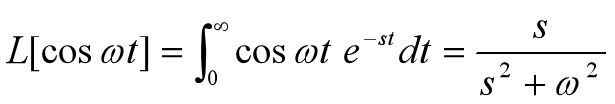
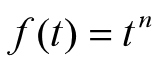

4、拉氏变换的性质
叠加定理
,齐次性和叠加性的组合起来就是拉氏变换的线形性质
微分定理
复微分定理
积分定理
位移定理
延迟定理
初值定理和终值定理
卷积定理
三、拉氏逆变换
四、matlab代码
%拉式变换 clc clear syms s t y=exp(-t)*cos(t); %原函数 LY=laplace(y) %拉氏变换 L_1=ilaplace(LY) %拉氏逆变换 e=L_1-y %做差检查结果是否正确 %原函数与象函数图像绘制 subplot(1,2,1) fplot(y);%原函数图像 title("原函数图像") legend("原函数") subplot(1,2,2) fplot(LY)%象函数图像 title("象函数图像") legend("象函数")

本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)