Python基于递归算法实现的汉诺塔与Fibonacci数列示例Pythonpython函数基础教程-

@本文来源于公众号：csdn2299，喜欢可以关注公众号 程序员学府
本文实例讲述了Python基于递归算法实现的汉诺塔与Fibonacci数列。给大家供大家参考，具体如下：

这里我们通过2个例子，学习python中递归的使用。

1. 找出Fibonacci数列中，下标为 n 的数（下标从0计数）

Fibonacci数列的形式是这样的：0,1,1,2,3,5,8,13……

① 使用while循环，python2代码如下：

def fib(n):   a,b=0,1   count=0   while count<n:     a,b=b,a+b     count=count+1   print a 

运行结果如下：

>>> fib(0) 0 >>> fib(1) 1 >>> fib(2) 1 >>> fib(3) 2 >>> fib(4) 3 >>> fib(5) 5 

② 使用递归（递归必须要有边界条件），python2代码如下：

def fib(n):   if n==0 or n==1:#递归的边界条件 return n   else:     return fib(n-1)+fib(n-2) 

运行结果如下：

>>> fib(0) 0 >>> fib(1) 1 >>> fib(2) 1 >>> fib(3) 2 >>> fib(4) 3 >>> fib(5) 5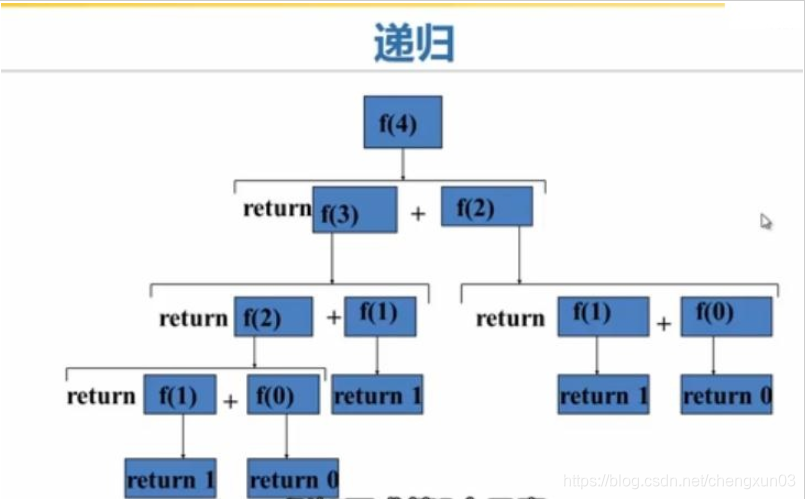 

递归是最能表现计算思维的算法之一，我们以f(4)为例，看一下递归的执行过程：
同一程序，使用递归虽然程序简洁，但递归的执行效率要比循环低，系统的资源消耗比循环大。因为递归是一层一层地往里面调用，结束后又一层一层地返回，所以递归的执行效率并不高。那为什么还要使用递归呢？因为有一些问题，我们找不到非常明显的循环方案，但容易找到明显的递归方案。比如说著名的汉诺塔问题。

2. 汉诺塔

下图是一个简化版的汉诺塔游戏，只有4个盘子：
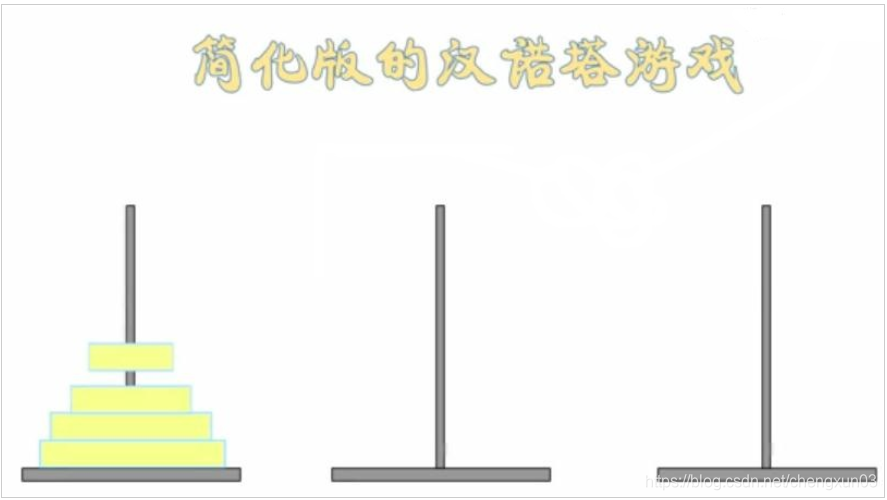
汉诺塔游戏规则如下：
python2代码如下：

def hanoi(a,b,c,n):   if n==1:#递归结束条件     print a,'->',c   else:     hanoi(a,c,b,n-1)     print a,'->',c     hanoi(b,a,c,n-1) 

运行结果：

>>> hanoi('A','B','C',1) A -> C >>> hanoi('A','B','C',2) A -> B A -> C B -> C >>> hanoi('A','B','C',3) A -> C A -> B C -> B A -> C B -> A B -> C A -> C 

非常感谢你的阅读
大学的时候选择了自学python，工作了发现吃了计算机基础不好的亏，学历不行这是
没办法的事，只能后天弥补，于是在编码之外开启了自己的逆袭之路，不断的学习python核心知识，深入的研习计算机基础知识，整理好了，如果你也不甘平庸，那就与我一起在编码之外，不断成长吧！
其实这里不仅有技术，更有那些技术之外的东西，比如，如何做一个精致的程序员，而不是“屌丝”，程序员本身就是高贵的一种存在啊，难道不是吗？[点击加入]想做你自己想成为高尚人，加油！