弹性鱼竿,即可以根据受力状态自由弯曲的鱼竿,如何实现“弯曲”是关键。说到弯曲,自然而然想到曲线,从曲线的角度出发,那么关键就是如何生成曲线,以及如何根据曲线修改物体形状,从而达到弯曲的效果。 贝塞尔曲线就不详细介绍了,具体可以参考百度百科。贝塞尔曲线简单来说就是通过n个控制点来生成曲线,而修改控制点位置可以修改曲线的形状。这里有个二阶贝塞尔曲线在线模拟工具,可以体验一下。 实现代码如下: 其中控制点可以使用n个空节点来代替,控制点的坐标即为空节点的坐标。至于t值,可以看作顶点到鱼竿底部的距离与整个鱼竿长度的比值,0<= t <=1。这样设计的话,我们第一个控制点P0应该在鱼竿底部位置,而最后一个控制点Pn应该在鱼竿顶部位置。 当然,按照上面公式计算出的只是一条曲线,而我们的目的是模型能按照这个曲线进行弯曲,如示意图: 可以看出,我们计算出来的曲线其实是图中的中心线,而mesh顶点应该位于中心线的两侧,所以顶点弯曲后的坐标是应该要由贝塞尔曲线计算的坐标经过一定变换得来。 代码如下: 这样我们就实现了通过控制点生成曲线,通过曲线弯曲物体的方法。如图: 接下来我们简单构造一个受力模型,通过物体施加拉力,拉力使控制点发生变化,从而使物体弯曲。我们简单设定一个Cube为施加拉力F的物体,然后为每个控制点设定一个完全弯曲所需要的力Fc,然后设定控制点朝拉力方向弯曲的角度为: 效果如图: 该方法做出来的弯曲效果还是很自然的,使用也比较简单,且不需要关节控制。但是比较吃性能,另外考虑到光照,顶点坐标更新后需要重新计算下mesh的法线信息normals。
一、实现思路
生成曲线的话,可以直接想到用贝塞尔曲线,由n个控制点绘制出n阶贝塞尔曲线,通过修改控制点的坐标来控制曲线变化。
然后我们可以考虑修改模型的Mesh顶点坐标来实现弯曲效果。
完成效果如下:
二、贝塞尔曲线公式
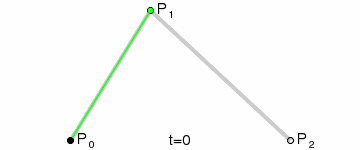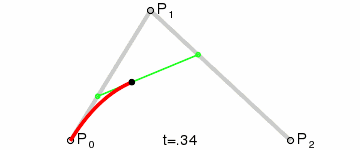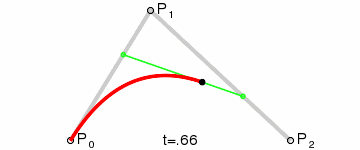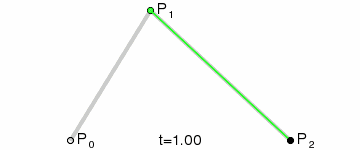
首先我们要实现贝塞尔曲线的计算公式,可知其n阶曲线的公式为:
//贝塞尔曲线公式 private Vector3 CalculateBezier(float t) { Vector3 ret = new Vector3(0, 0, 0); int n = 阶数; for(int i = 0; i <= n; i++) { Vector3 pi = 第i个控制点的坐标; ret = ret + Mathf.Pow(1 - t, n - i) * Mathf.Pow(t, i) * Cn_m(n, i) * pi; } return ret; } //组合数方程 private int Cn_m(int n, int m) { int ret = 1; for(int i = 0; i < m; i++){ ret = ret * (n - i) / (i + 1); } return ret; } 三、模型应用曲线

经过观察可以发现,弯曲后顶点的坐标P’应由计算出的曲线上的坐标P进行两次偏移得出:在该点法线方向上进行偏移
a、在垂直于弯曲面的方向上进行偏移
b。
// 对原来的顶点做贝塞尔曲线变换,得到弯曲变换后对应的点位置 private void UpdateBezierBend() { oriVertices = 模型未弯曲时的顶点数组; topPos = 最后一个控制点的坐标,用来计算模型长度; bendVector = 弯曲方向; for(int i = 0; i < oriVertices.Length; i++) { //获取顶点坐标,计算t值 Vector3 oriPos = oriVertices[i]; float t = oriPos.y / topPos.y; //获取顶点在贝塞尔曲线上对应的坐标 Vector3 p = CalculateBezier(t); //获取顶点在曲线上应有的法线偏移向量 Vector3 vectorA = GetBendNormalVector(t, oriPos, bendVector); //获取顶点在曲线上应有的垂直偏移向量 Vector3 vectorB = new Vector3(oriPos.x, 0, oriPos.z) - Vector3.Project(new Vector3(oriPos.x, 0, oriPos.z), bendVector); //获取顶点最终弯曲位置 vector3 p' = p + vectorA + vectorB; } todo-修改顶点坐标; } // 获取指定点上的法向量偏移 private Vector3 GetBendNormalVector(float t, Vector3 oriPos, Vector3 bendVector) { Vector3 tangentVector = CalculateBezierTangent(t);//切线斜率 Vector3 normalVector = 由法线和切线互相垂直计算出法线方向; //法线向量的模应为到投影到弯曲面后,到中心点的距离 float magnitude = Vector3.Project(new Vector3(oriPos.x, 0, oriPos.z), bendVector).magnitude; normalVector = normalVector.normalized * magnitude; return normalVector; } //对曲线公式求导得出切线向量 private Vector3 CalculateBezierTangent(float t) { Vector3 ret = new Vector3(0, 0, 0); int n = 阶数; for(int i = 0; i <= n; i++) { Vector3 pi = 第i个控制点的坐标; ret = ret + (-1 * (n - i) * Mathf.Pow(1 - t, n - i - 1) * Mathf.Pow(t, i) * Cn_m(n, i) * pi + i * Mathf.Pow(1 - t, n - i) * Mathf.Pow(t, i - 1) * Cn_m(n, i) * pi); } return ret; }
四、简单构造受力模型
a = Mathf.Clamp(F/Fc, 0, 1.0) * 拉力与控制点的夹角;
为了模拟比较真实的弯曲效果,Fc可以看成每节竿子的弹力大小,越靠近底部的控制点Fc就越大,越难弯曲,反之,越靠近竿顶的控制点Fc越小,也就越容易弯曲。
代码如下:private void UpdateControlPoint() { float F = Cube.force; //根据受力计算各个控制点旋转角度 n = 控制点数量; for(int i = 1; i < n - 1; i++)//第一个和最后一个点不计算弯曲 { //计算最大弯曲方向 Vector3 toVector = 施力物体相对控制点pi的方向; Quaternion maxRotation = Quaternion.FromToRotation(Vector3.up, toVector); //计算弯曲比例 float rotateRate = Mathf.Clamp(F / Fc, 0f, 1.0f); //设置旋转角度 pi.localRotation = Quaternion.Lerp(Quaternion.Euler(0, 0, 0), maxRotation, rotateRate); } }
五、最后
附上源码:https://github.com/dxxia/TestFishRod_BezierMesh
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)